练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    14．解不等式：|x-2|＜|x+1|

    分析 分为三种情况，去掉绝对值符号，求出每种情况的不等式的解集即可．

    解答 解：①当x≥2时，原不等式化为：x-2＜x+1，
    -2＜1，
    此时x为全体实数，即x≥2；
    ②当-1＜x＜2时，原不等式化为：2-x＜x+1，
    x＜$\frac{1}{2}$，
    即$\frac{1}{2}$＜x＜2；
    ③当x≤-1时，原不等式化为：2-x＜-（x+1），
    此时不等式无解；
    所以原不等式的解集为x$＞\frac{1}{2}$．

    点评 本题考查了解一元一次不等式，绝对值的应用，能求出符合条件的所有情况是解此题的关键，用了分类讨论思想．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    19．如图，三角形A′B′C′是由三角形ABC沿射线AC方向平移2cm得到的，若AC=3cm，则A′C=1cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

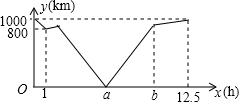    5．一辆快车从甲地开往乙地，一辆慢车从乙地开往甲地，两车同时出发，分别以各自的速度在甲乙两地间匀速行驶，行驶1小时后，快车司机发现有重要文件遗忘在出发地，便立即返回出发地，拿上文件后（取文件时间不计）立即再从甲地开往乙地，结果快车先到达乙地，慢车继续行驶到甲地．设慢车行驶时间x（h），两车之间的距离为y（km），y与x的函数图象如图所示，则a=7．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．东南花都某花卉展区拟设计一个边界用篱笆围成的扇形花圃．
    （1）若花圃的设计面积为36m2，则扇形的半径为多少米时，所用的篱笆最短，最短的篱笆是多少米？
    （2）现有一段36m的篱笆用来围成这个花圃，问扇形的半径应设计为多少米时，花圃的面积最大，最大面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    9．已知函数y=（k-1）x+2k-4，当k=2时，图象过原点，当k＜1时，函数值y随x的增大而减小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．如图，直线l过正方形ABCD的顶点B，点A、点C到直线l的距离分别是3和4，则该正方形中AC的长是5$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

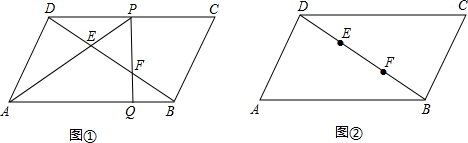
    6．E、F为?ABCD的对角线DB上三等分点，连AE并延长交DC于P，连PF并延长交AB于Q，如图①
    （1）在备用图中，画出满足上述条件的图形，记为图②，试用刻度尺在图①、②中量得AQ、BQ的长度，估计AQ、BQ间的关系，并填入下表长度单位：cm
    AQ长度BQ长度AQ、BQ间的关系
    图①中2.70.9AQ=3BQ
    图②中3.31.1AQ=3BQ
    由上表可猜测AQ、BQ间的关系是AQ=3BQ
    （2）上述（1）中的猜测AQ、BQ间的关系成立吗？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．已知，如图长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    4．对于不相等的两个实数a，b，定义运算“*”如下：a*b=$\frac{\sqrt{a}}{a-b}$，例如2*1=$\frac{\sqrt{2}}{2-1}$=$\sqrt{2}$，则式子3*（1-x）有意义的条件是x≠-2．

    查看答案和解析>>

    同步练习册答案