
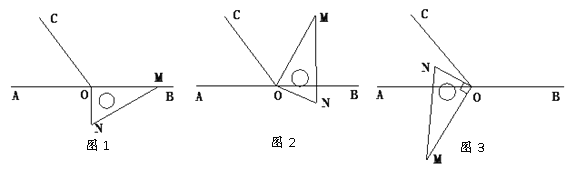
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=112°.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.
(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC,问:直线ON是否平分∠AOC?请说明理由;
(2)将图1中的三角板绕点O按每秒4°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为多少?
(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究:∠AOM与∠NOC之间的数量关系,并说明理由.
【答案】(1)平分;(2)(2)t=59或14 (3)∠AOM-∠NOC=220
【解析】
试题(1)根据角平分线的定义和平角的定义求出∠COP=30°,即可证得直线ON平分∠AOC;
(2)当ON绕O点旋转至图②位置时,此时ON转过60°,旋转时间为10秒;当ON转至锐角∠AOC内部平分∠AOC时,ON转过90°+150°=240°,旋转时间为40秒;
(3)根据∠AOM+∠AON=90°,∠AON+∠NOC=60°,得到∠AOM一∠NOC =30°.
试题解析:(1)直线ON平分∠AOC(如图),理由如下:
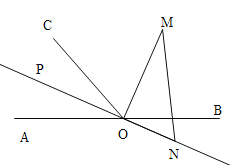
∵OM平分∠BOC,且∠BOC=120°,
∴∠COM=60°,
又∠MON=90°,
∴∠POM=90°,
∴∠COP=30°,
又∠AOC=60°,
∴OP平分∠AOC,
即直线ON平分∠AOC.
(2)当ON绕O点旋转至图②位置时,ON平分∠AOC,此时ON转过60°,
当ON转至锐角∠AOC内部平分∠AOC时,ON转过90°+150°=240°,
所以t=10或40(秒) ,
答:旋转时间t的值为10秒或40秒.
(3) ∠AOM—∠NOC=30°,
∵∠AOM+∠AON=90°,
∠AON+∠NOC=60°,
∴∠AOM一∠NOC =30°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列命题中,假命题有( )
①两点之间线段最短;
②到角的两边距离相等的点在角的平分线上;
③过一点有且只有一条直线与已知直线平行;
④垂直于同一直线的两条直线平行;
⑤若![]() 的弦AB,CD交于点P,则
的弦AB,CD交于点P,则![]()
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若中学生体质健康综合评定成绩为x分,满分为100分.规定:85≤x≤100为A级,75≤x<85为B级,60≤x<75为C级,x<60为D级.现随机抽取某中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图.
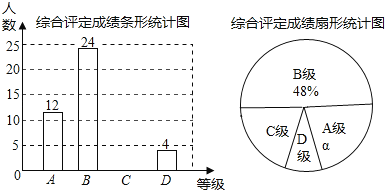
请根据图中的信息,解答下列问题:
(1)在这次调查中,一共抽取了 名学生;a= %;C级对应的圆心角为 度.
(2)补全条形统计图;
(3)若该校共有2000名学生,请你估计该校D级学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由大小相同(棱长为1分米)的小立方块搭成的几何体如下图.


(1)请在右图的方格中画出该几何体的俯视图和左视图;
(2)图中有 块小正方体,它的表面积(含下底面)为 ;
(3)用小立方体搭一几何体,使得它的俯视图和左视图与你在上图方格中所画的图一致,则这样的几何体最少要_______个小立方块,最多要_______个小立方块.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系图象如图所示,根据图中提供的信息,有下列说法:

(1)他们都行驶了18千米;
(2)甲在途中停留了0.5小时;
(3)乙比甲晚出发了0.5小时;
(4)相遇后,甲的速度小于乙的速度;
(5)甲、乙两人同时到达目的地
其中符合图象描述的说法有( )
A. 2个B. 3个C. 4个D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“我的中国梦”演讲比赛活动,九(1)、九(2)班根据初赛成绩各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如下图所示.
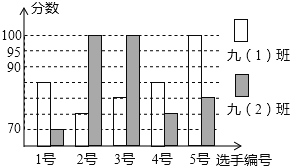
(1)根据如图,分别求出两班复赛的平均成绩和方差;
(2)根据(1)的计算结果,分析哪个班级5名选手的复赛成绩波动小?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,飞机在一定高度上沿水平直线飞行,先在点![]() 处测得正前方小岛
处测得正前方小岛![]() 的俯角为
的俯角为![]() ,面向小岛方向继续飞行
,面向小岛方向继续飞行![]()
![]() 到达
到达![]() 处,发现小岛在其正后方,此时测得小岛的俯角为
处,发现小岛在其正后方,此时测得小岛的俯角为![]() .如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).
.如果小岛高度忽略不计,求飞机飞行的高度(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,用三种大小不同的5个正方形和一个长方形(阴影部分)拼成长方形ABCD,其中EF=2厘米,最小的正方形的边长为x厘米.
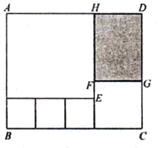
(1)用含x的代数式表示FG=________厘米,DG=________厘米.
(2)若长方形ABCD的周长等于52,求x的值
(3)若FG:DG=2:3,求四边形FGDH(阴影部分)的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com