
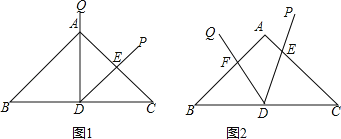
����Ŀ���ڵ�����ABC�У�AB=AC=10��BC=12��DΪ�ױ�BC���е㣬��DΪ����Ľǡ�PDQ=��B��
��1����ͼ1��������DQ������A��DP��AC���ڵ�E��ֱ��д�����CDE���Ƶ������Σ�
��2����ͼ2��������DQ��AB�ڵ�F��DP��AC���ڵ�E����AF=x��AEΪy����д��y��x�ĺ�����ϵʽ������Ҫ��д���Ա�����ȡֵ��Χ��
��3���ڣ�2���������£�����EF�����DEF���CDE��������˵�����ɣ�
���𰸡���1����1�����CDE���Ƶ�������Ϊ��ABD����ACD����ADE�����ɼ���������2��y=![]() ����3����DEF���CDE���ƣ����ɼ�����.
����3����DEF���CDE���ƣ����ɼ�����.
�����������������1���ɵ��������ε����ʵó���B=��C����ADB=��ADC=90���������ABD�ס�ACD��֤����PDQ=��C���ɡ�DAE=��CAD���ó���ADE�ס�ACD����֤����CDE�ס�CAD�����ɵó������
��2��֤����BDF�ס�CDE���ó���Ӧ�߳ɱ���![]() �����ɵó�y��x�ĺ�����ϵʽ��
�����ɵó�y��x�ĺ�����ϵʽ��
��3���ɣ�2����֪����BDF�ס�CDE���ó�![]() ֤��
֤��![]() ���ɡ�EDF=��C�����ɵó���DEF�ס�CED��
���ɡ�EDF=��C�����ɵó���DEF�ס�CED��
�����������1������CDE���Ƶ�������Ϊ��ABD����ACD����ADE���������£�
��AB=AC��DΪ�ױ�BC���е㣬
���B=��C��AD��BC��
���ADB=��ADC=90����
���ABD�ס�ACD��
�ߡ�PDQ=��B��
���PDQ=��C��
�֡ߡ�DAE=��CAD��
���ADE�ס�ACD��
�ߡ�CDE+��PDQ=90����
���C+��PDQ=90����
���CED=90��=��ADC��
�֡ߡ�C=��C��
���CDE�ס�CAD��
�����ABD�ס�ACD�ס�ADE�ס�CDE��
��2���ߡ�FDC=��B+��BDF��
��FDC=��FDE+��EDC��
���EDC=��BDF��
���BDF�ס�CDE��
��![]() ��
��
��DΪBC���е㣬
��BD=CD=6��
��![]()
��y=![]() ��
��
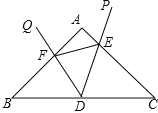
��3����DEF����CDE���ƣ��������£���ͼ��ʾ��
�ɣ�2����֪����BDF�ס�CDE��
��![]() ��
��
��BD=CD��
��![]() ��
��
�֡ߡ�EDF=��C��
���DEF�ס�CED��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AE��AB��AE=AB��BC��CD��BC=CD���밴��ͼ������ע�����ݣ���ͼ��ʵ����Χ�ɵ�ͼ�ε����S��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����и����߶������һ�������ε��ǣ� ����
A.3cm��3cm��6cmB.2cm��3cm��6cm
C.5cm��8cm��12cmD.4cm��7cm��11cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�MΪBC��һ�㣬F��AM���е㣬EF��AM������ΪF����AD���ӳ����ڵ�E����DC�ڵ�N��
��1����֤����ABM �ס�EFA��
��2����AB=12��BM=5����DE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��a��0���IJ���ͼ���䶥������Ϊ��1��n��������x���һ�������ڵ㣨3��0���ͣ�4��0��֮�䣮�����н��ۣ���a��b+c��0����3a+b=0����b2=4a��c��n������һԪ���η���ax2+bx+c=n��1����������ȵ�ʵ������������ȷ�����ǣ�������

A. �٢ڢ� B. �٢ۢ� C. �ۢܢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��a+b��2=144�� ��a-b��2=36�� ��ab=______��a2 + b2=_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����OABC�Ķ���A��C������ֱ�Ϊ��10��0������0��4������D��OA���е㣬��P��BC���˶�������ODP������Ϊ5�ĵ���������ʱ����P������Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A����1��2������y��ĶԳƵ��ڣ�������
A. ��һ���� B. �ڶ����� C. �������� D. ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��������ʵij������飬�����������ר���Ĵ�ʽ�ܵ����ڻ�ӭ�����˽��ڷǸ߷���ʱ��ij��ר������ȡ�ķ���![]() ��Ԫ������ʻ���
��Ԫ������ʻ���![]()
![]() �ĺ�����ϵ��ͼ��ʾ�������ͼ�����������⣺
�ĺ�����ϵ��ͼ��ʾ�������ͼ�����������⣺
��![]() ����
����![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��![]() ����ר���ͻ���ʻ��ʱ��
����ר���ͻ���ʻ��ʱ��![]() ����ÿ��������
����ÿ��������![]() Ԫ�ĵ��ٷѣ�����
Ԫ�ĵ��ٷѣ�����![]() ���ӵIJ��ְ�
���ӵIJ��ְ�![]() ���Ӽ��㣩��ij�˿���һ���ڷǸ߷��ڳ���ר����;�е�����ʻ��
���Ӽ��㣩��ij�˿���һ���ڷǸ߷��ڳ���ר����;�е�����ʻ��![]() ���ӣ�������
���ӣ�������![]() Ԫ������λ�˿���ר������ʻ��̣�
Ԫ������λ�˿���ר������ʻ��̣�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com