
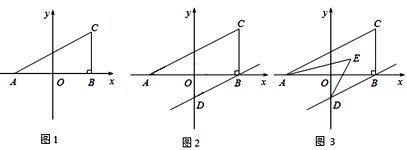
【题目】如图1,在平面直角坐标系中,A(a,0),C(b,2),且满足![]() ,过C作
,过C作![]() 轴于B,
轴于B,
(1)求a,b的值;
(2)在y轴上是否存在点P,使得△ABC和△OCP的面积相等,若存在,求出点P坐标,若不存在,试说明理由.
(3)若过B作BD∥AC交y轴于D,且AE,DE分别平分∠CAB,∠ODB,如图2,图3,
①求:∠CAB+∠ODB的度数;
②求:∠AED的度数.
【答案】(1)a=-2,b=2;(2)P(0,-4)或(0,4);(3)①∠CAB+∠ODB=90°;②∠AED=45°.
【解析】
(1)根据非负数的性质即可求得a、b的值;(2)先求得S△ABC=4,设P(0,t),根据S△OPC=![]() OP×2=
OP×2=![]() ×
×![]() ×2=4求得t值,即可求得点P的坐标;(3)①已知BD∥AC,根据两直线平行,内错角相等可得∠CAB=∠OBD,由∠OBD+∠ODB=90°,即可得∠CAB+∠ODB=90°;②根据角平分线的定义及①中的结论,可求得∠3+∠4=45°;过点E作EF∥AC,即可得EF∥BD∥AC,根据平行线的性质可得∠3=∠1,∠2=∠4,由此求得∠AED=∠1+∠2=∠4+∠3=45°.
×2=4求得t值,即可求得点P的坐标;(3)①已知BD∥AC,根据两直线平行,内错角相等可得∠CAB=∠OBD,由∠OBD+∠ODB=90°,即可得∠CAB+∠ODB=90°;②根据角平分线的定义及①中的结论,可求得∠3+∠4=45°;过点E作EF∥AC,即可得EF∥BD∥AC,根据平行线的性质可得∠3=∠1,∠2=∠4,由此求得∠AED=∠1+∠2=∠4+∠3=45°.
(1)∵![]() ,
,
∴a+2=0,b-2=0,
∴a=-2,b=2;
(2)∵a=-2,b=2,
∴A(-2,0),C(2,2),
∴S△ABC=![]() ABBC=
ABBC=![]() ×4×2=4;
×4×2=4;
设P(0,t),
∴S△OPC=![]() OP×2=
OP×2=![]() ×
×![]() ×2=
×2=![]() =4;
=4;
∴t=4或t=-4,
∴P(0,-4)或(0,4).
(3)①∵BD∥AC,
∴∠CAB=∠OBD,
∵∠OBD+∠ODB=90°,
∴∠CAB+∠ODB=90°;
②∵AE,DE分别平分∠CAB,∠ODB,
∴∠3=![]() ,∠4=
,∠4=![]() ,
,
∵∠CAB+∠ODB=90°,
∴∠3+∠4=![]() +
+![]() =45°,
=45°,
过点E作EF∥AC,

∵BD∥AC,
∴EF∥BD∥AC,
∴∠3=∠1,∠2=∠4,
∴∠AED=∠1+∠2=∠4+∠3=45°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】A,B两地相距120km.甲、乙两辆汽车同时从A地出发去B地,已知甲车的速度是乙车速度的1.2倍,结果甲车比乙车提前20分钟到达,求甲车的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一块直角三角形的绿地,量得直角边BC为6cm,AC为8cm,现在要将原绿地扩充后成等腰三角形,且扩充的部分是以AC为直角边的直角三角形,求扩充后的等腰三角形绿地的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB≠AC.D、E分别为边AB、AC上的点.AC=3AD,AB=3AE,点F为BC边上一点,添加一个条件: , 可以使得△FDB与△ADE相似.(只需写出一个) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的边长为3,点A、C分别在x轴,y轴的正半轴上,点D(1,0)在OA上,P是OB上一动点,则PA+PD的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,每个小正方形的边长为1个单位,每个小方格的顶点叫格点.
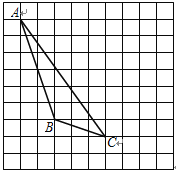
(1)画出△ABC向右平移4个单位后得到的△A1B1C1;
(2)图中AC与A1C1的关系是: _____________.
(3)画出△ABC的AB边上的高CD;垂足是D;
(4)图中△ABC的面积是_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:把形如ax2+bx+c的二次三项式(或其一部分)配成完全平方式的方法叫做配方法,配方法的基本形式是完全平方公式的逆写,即a2±2ab+b2=(a±b)2,例如二次三项式x2-2x+9的配方过程如下:x2-2x+9=x2-2x+1-1+9=(x-1)2+8.
请根据阅读材料解决下列问题:
(1)比照上面的例子,将下面的两个二次三项式分别配方:
①x2-4x+1=______;
②3x2+6x-9=3(x2+2x)-9=______;
(2)已知x2+y2-6x+10y+34=0,求3x-2y的值;
(3)已知a2+b2+c2+ab-3b+2c+4=0,求a+b+c的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
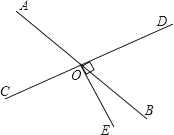
【题目】如图,AB和CD相交于点O,∠DOE=90°,若∠BOE=![]() ∠AOC,
∠AOC,
(1)指出与∠BOD相等的角,并说明理由.
(2)求∠BOD,∠AOD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富少年儿童的业余生活,某社区要在如图所示AB所在的直线建一图书室,本社区有两所学校所在的位置在点C和点D处,CA⊥AB于A,DB⊥AB于B,已知AB=25km,CA=15km,DB=10km,试问:图书室E应该建在距点A多少km处,才能使它到两所学校的距离相等?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com