
【题目】如图,已知∠A=∠AGE,∠D=∠DGC. 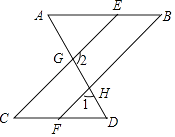
(1)求证:AB∥CD;
(2)若∠2+∠1=180°,且∠BEC=2∠B+30°,求∠C的度数.
【答案】
(1)证明:∵∠A=∠AGE,∠D=∠DGC,
又∵∠AGE=∠DGC,
∴∠A=∠D,
∴AB∥CD
(2)证明:∵∠1+∠2=180°,
又∵∠CGD+∠2=180°,
∴∠CGD=∠1,
∴CE∥FB,
∴∠C=∠BFD,∠CEB+∠B=180°.
又∵∠BEC=2∠B+30°,
∴2∠B+30°+∠B=180°,
∴∠B=50°.
又∵AB∥CD,
∴∠B=∠BFD,
∴∠C=∠BFD=∠B=50°
【解析】(1)欲证明AB∥CD,只需推知∠A=∠D即可;(2)利用平行线的判定定理推知CE∥FB,然后由平行线的性质、等量代换推知∴∠C=∠BFD=∠B=50°.
【考点精析】认真审题,首先需要了解平行线的判定(同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行).


科目:初中数学 来源: 题型:
【题目】直线MN与直线PQ垂直相交于O,点A在直线PQ上运动,点B在直线MN上运动.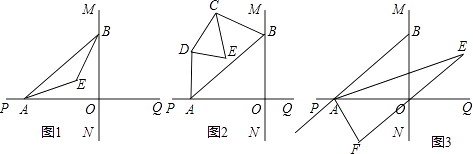
(1)如图1,已知AE、BE分别是∠BAO和∠ABO角的平分线,点A、B在运动的过程中,∠AEB的大小是否会发生变化?若发生变化,请说明变化的情况;若不发生变化,试求出∠AEB的大小.
(2)如图2,已知AB不平行CD,AD、BC分别是∠BAP和∠ABM的角平分线,又DE、CE分别是∠ADC和∠BCD的角平分线,点A、B在运动的过程中,∠CED的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出其值.
(3)如图3,延长BA至G,已知∠BAO、∠OAG的角平分线与∠BOQ的角平分线及延长线相交于E、F,在△AEF中,如果有一个角是另一个角的3倍,试求∠ABO的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长:中华汉字,寓意深广。为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分。为了更好地了解本次大赛的成绩分布情况,随机抽取了200名学生的成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
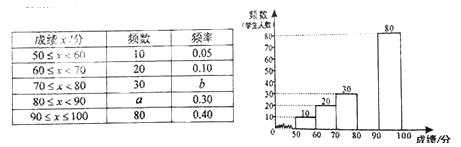
请根据所给的信息,解答下列问题:
(1)a= ,b= ;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数会落在 分数段;
(4)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等的大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=20°,∠ACP=50°,则∠A+∠P=( ) 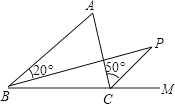
A.70°
B.80°
C.90°
D.100°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司到果园基地购买某种优质水果,慰问医务工作者,果园基地对购买量在3000千克以上(含3000千克)的有两种销售方案,甲方案:每千克9元,由基地送货上门。乙方案:每千克8元,由顾客自己租车运回,已知该公司租车从基地到公司的运输费为5000元。
(1)分别写出该公司两种购买方案的付款y(元)与所购买的水果质量x(千克)之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)依据购买量判断,选择哪种购买方案付款最少?并说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com