
 教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-$\frac{1}{10}$(x-4)2+3,由此可知铅球推出的距离是(4+$\sqrt{30}$)m.
教练对小明推铅球的录像进行技术分析,发现铅球行进高度y(m)与水平距离x(m)之间的关系为y=-$\frac{1}{10}$(x-4)2+3,由此可知铅球推出的距离是(4+$\sqrt{30}$)m.  智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{a+b}{ab}$ | B. | $\frac{ab}{2(a+b)}$ | C. | $\frac{a+b}{2ab}$ | D. | $\frac{ab}{a+b}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
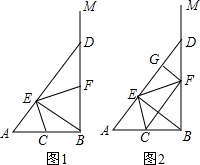 如图,∠ABM为直角,点C为线段BA的中点,点D是射线BM上的一个动点(不与点B重合),连结AD,作BE⊥AD,垂足为E,连结CE,过点E作EF⊥CE,交BD于F.
如图,∠ABM为直角,点C为线段BA的中点,点D是射线BM上的一个动点(不与点B重合),连结AD,作BE⊥AD,垂足为E,连结CE,过点E作EF⊥CE,交BD于F.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,符合图象的解析式是④.(填序号)
如图,符合图象的解析式是④.(填序号)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B点的坐标为(-1,1),将△ABC绕着点C顺时针旋转90°,则点A的对应点的坐标为(5,-1).
如图,每个小正方形的边长均为1,△ABC的三个顶点都是网格线的交点,已知B点的坐标为(-1,1),将△ABC绕着点C顺时针旋转90°,则点A的对应点的坐标为(5,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (m+n)(-m+n) | B. | (x3-y3)(x3+y3) | C. | (-a-b)(a+b) | D. | ( $\frac{1}{3}$a-b)( $\frac{1}{3}$a+b) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1-3x}{2}$-3=2x+3 | B. | $\frac{3(1-3x)}{2}$-3=2x | C. | 3(1-3x)-6=4x | D. | 3(1-3x)-4x=6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com