
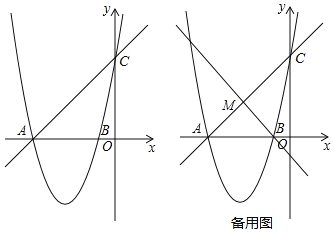
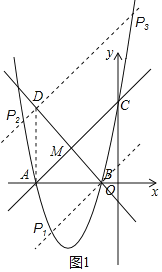
ЁОЬтФПЁПШчЭМЃЈ1ЃЉЃЌХзЮяЯпyЃНax2+6x+cНЛxжсгкAЃЌBСНЕуЃЌНЛyжсгкЕуCЃЎжБЯпyЃНx+5ОЙ§ЕуAЃЌCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМЃЈ2ЃЉЃЌШєЙ§ЕуBЕФжБЯпНЛжБЯпACгкЕуMЃЎ
ЂйЕБBMЁЭACЪБЃЌЙ§ХзЮяЯпЩЯвЛЖЏЕуPЃЈВЛгыЕуBЃЌCжиКЯЃЉЃЌзїжБЯпBMЕФЦНааЯпНЛACгкЕуQЃЌШєвдЕуBЃЌMЃЌQЃЌPЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЌЧѓЕуPЕФКсзјБъЃЛ
ЂкСЌНсBCЃЌЕБжБЯпBMгыжБЯпACЕФМаНЧЕШгкЁЯACBЕФ2БЖЪБЃЌЧыжБНгаДГіЕуMЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉyЃНx2+6x+5ЃЛЃЈ2ЃЉЂйЕуPЕФКсзјБъЮЊЉ4ЃЌ![]() Лђ
Лђ![]() ЃЛЂкЕуMЕФзјБъЮЊЃЈ
ЃЛЂкЕуMЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУвЛДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїПЩЧѓГіЕуAЃЌCЕФзјБъЃЌгЩЕуAЃЌCЕФзјБъРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉРћгУЖўДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїПЩЧѓГіЕуBЕФзјБъЃЛ
ЂйЗжЫФБпаЮBMQPЮЊЦНааЫФБпаЮКЭЫФБпаЮBMPQЮЊЦНааЫФБпаЮСНжжЧщПіПМТЧЃКЃЈiЃЉЕБЫФБпаЮBMQPЮЊЦНааЫФБпаЮЪБЃЌЙ§ЕуBзїBP1ЁЮACЃЌНЛХзЮяЯпгкЕуP1ЃЌгЩжБЯпACЕФНтЮіЪННсКЯЕуBЕФзјБъПЩЕУГіжБЯпBP1ЕФНтЮіЪНЃЌСЊСЂжБЯпBP1КЭХзЮяЯпЕФНтЮіЪНГЩЗНГЬзщЃЌЭЈЙ§НтЗНГЬзщПЩЕУГіЕуP1ЕФКсзјБъЃЛЃЈiiЃЉЕБЫФБпаЮBMPQЮЊЦНааЫФБпаЮЪБЃЌЙ§ЕуAзїADЁЮyжсЃЌНЛжБЯпBMгкЕуDЃЌвзЧѓЕуDЕФзјБъЮЊЃЈЉ5ЃЌ4ЃЉЃЌЙ§ЕуDзїжБЯпP2P3ЁЮACЃЌНЛХзЮяЯпгкЕуP2ЃЌP3ЃЌгЩжБЯпACЕФНтЮіЪННсКЯЕуDЕФзјБъПЩЕУГіжБЯпP2P3ЕФНтЮіЪНЃЌСЊСЂжБЯпP2P3КЭХзЮяЯпЕФНтЮіЪНГЩЗНГЬзщЃЌЭЈЙ§НтЗНГЬзщПЩЧѓГіЕуP2ЃЌP3ЕФКсзјБъЃЛ
ЂкзїBCЕФДЙжБЦНЗжЯпlЃЌДЙзуЮЊEЃЌНЛACгкЕуM1ЃЌзїBNЁЭACгкЕуNЃЌзїЕуM1ЙигкЕуNЕФЖдГЦЕуM2ЃЌM1ЃЌM2ЗћКЯЬѕМўЃЌгЩЕуBЃЌCЕФзјБъПЩЧѓГіжБЯпBCЕФНтЮіЪНМАЕуEЕФзјБъЃЌНсКЯжБЯпlЁЭBCПЩЧѓГіжБЯпlЕФНтЮіЪНЃЌСЊСЂжБЯпlКЭжБЯпACЕФНтЮіЪНГЩЗНГЬзщЃЌЭЈЙ§НтЗНГЬзщПЩЧѓГіЕуM1ЕФзјБъЃЛгЩжБЯпACЕФНтЮіЪНЁЂЕуBЕФзјБъМАBNЁЭACПЩЧѓГіжБЯпONЕФНтЮіЪНЃЌСЊСЂжБЯпONКЭжБЯпACЕФНтЮіЪНГЩЗНГЬзщЃЌЭЈЙ§НтЗНГЬзщПЩЧѓГіЕуNЕФзјБъЃЌдйНсКЯЕуNЮЊЯпЖЮM1M2ЕФжаЕуПЩЧѓГіЕуM2ЕФзјБъЃЎ
ЃЈ1ЃЉЕБxЃН0ЪБЃЌyЃНx+5ЃН5ЃЌ
ЁрЕуCЕФзјБъЮЊЃЈ0ЃЌ5ЃЉЃЛ
ЕБyЃН0ЪБЃЌx+5ЃН0ЃЌ
НтЕУЃКxЃНЉ5ЃЌ
ЁрЕуAЕФзјБъЮЊЃЈЉ5ЃЌ0ЃЉЃЎ
НЋAЃЈЉ5ЃЌ0ЃЉЃЌCЃЈ0ЃЌ5ЃЉДњШыyЃНax2+6x+cЃЌЕУЃК
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃНx2+6x+5ЃЎ
ЃЈ2ЃЉЕБyЃН0ЪБЃЌx2+6x+5ЃН0ЃЌ
НтЕУЃКx1ЃНЉ5ЃЌx2ЃНЉ1ЃЌ
ЁрЕуBЕФзјБъЮЊЃЈЉ1ЃЌ0ЃЉЃЎ
ЂйЁпPQЁЮBMЃЌ
ЁрЗжСНжжЧщПіПМТЧЃЌШчЭМ1ЫљЪОЃК
ЃЈiЃЉЕБЫФБпаЮBMQPЮЊЦНааЫФБпаЮЪБЃЌЙ§ЕуBзїBP1ЁЮACЃЌНЛХзЮяЯпгкЕуP1ЃЎ
ЁпжБЯпACЕФНтЮіЪНЮЊyЃНx+5ЃЌ
ЁрЩшжБЯпBP1ЕФНтЮіЪНЮЊyЃНx+bЃЌ
НЋBЃЈЉ1ЃЌ0ЃЉДњШыyЃНx+bЃЌЕУЃКЉ1+bЃН0ЃЌ
НтЕУЃКbЃН1ЃЌ
ЁржБЯпBP1ЕФНтЮіЪНЮЊyЃНx+1ЃЎ
СЊСЂжБЯпBP1КЭХзЮяЯпЕФНтЮіЪНГЩЗНГЬзщЃЌЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК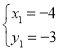 ЃЌ
ЃЌ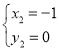 ЃЌ
ЃЌ
ЁрЕуP1ЕФКсзјБъЮЊЉ4ЃЛ
ЃЈiiЃЉЕБЫФБпаЮBMPQЮЊЦНааЫФБпаЮЪБЃЌЙ§ЕуAзїADЁЮyжсЃЌНЛжБЯпBMгкЕуDЃЌЙ§ЕуDзїжБЯпP2P3ЁЮACЃЌНЛХзЮяЯпгкЕуP2ЃЌP3ЃЎ
ЁпOAЃНOCЃЌ
ЁрЁЯOACЃН45ЁуЃЎ
ЁпBMЁЭACЃЌDAЁЭABЃЌ
ЁрЁЯAMBЃН90ЁуЃЌЁЯABMЃН45ЁуЃЌЁЯADMЃН45ЁуЃЎ
дкЁїAMDКЭЁїAMBжаЃЌ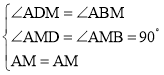 ЃЌ
ЃЌ
ЁрЁїAMDЁеЁїAMBЃЈAASЃЉЃЌ
ЁрADЃНABЃЌDMЃНBMЃЎ
ЁрЕуDЕФзјБъЮЊЃЈЉ5ЃЌ4ЃЉЃЎ
гжЁпжБЯпACЕФНтЮіЪНЮЊyЃНx+5ЃЌ
ЁржБЯпP2P3ЕФНтЮіЪНЮЊyЃНx+9ЃЎ
СЊСЂжБЯпP2P3КЭХзЮяЯпЕФНтЮіЪНГЩЗНГЬзщЃЌЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК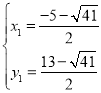 ЃЌ
ЃЌ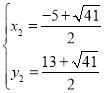 ЃЌ
ЃЌ
ЁрЕуP2ЕФКсзјБъЮЊ![]() ЃЌЕуP3ЕФКсзјБъЮЊ
ЃЌЕуP3ЕФКсзјБъЮЊ![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃКЕуPЕФКсзјБъЮЊЉ4ЃЌ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
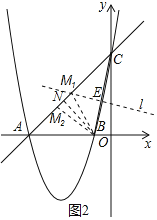
ЃЈ3ЃЉзїBCЕФДЙжБЦНЗжЯпlЃЌДЙзуЮЊEЃЌНЛACгкЕуM1ЃЌзїBNЁЭACгкЕуNЃЌзїЕуM1ЙигкЕуNЕФЖдГЦЕуM2ЃЌM1ЃЌM2ЗћКЯЬѕМўЃЎШчЭМ2ЫљЪОЃЎ
ЁпЕуBЕФзјБъЮЊЃЈЉ1ЃЌ0ЃЉЃЌЕуCЕФзјБъЮЊЃЈ0ЃЌ5ЃЉЃЌ
ЁрЕуEЕФзјБъЮЊЃЈЉ![]() ЃЌ
ЃЌ![]() ЃЉЃЌжБЯпBCЕФНтЮіЪНЮЊyЃН5x+5ЃЌ
ЃЉЃЌжБЯпBCЕФНтЮіЪНЮЊyЃН5x+5ЃЌ
ЁржБЯпlЕФНтЮіЪНЮЊyЃНЉ![]() x+
x+![]() ЃЎ
ЃЎ
СЊСЂжБЯпlКЭжБЯпACЕФНтЮіЪНГЩЗНГЬзщЃЌЕУЃК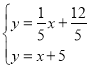 ЃЌ
ЃЌ
НтЕУЃК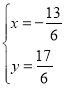 ЃЌ
ЃЌ
ЁрЕуM1ЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁпжБЯпACЕФНтЮіЪНЮЊyЃНx+5ЃЌЕуBЕФзјБъЮЊЃЈЉ1ЃЌ0ЃЉЃЌBNЁЭACЃЌ
ЁржБЯпONЕФНтЮіЪНЮЊyЃНЉxЉ1ЃЎ
СЊСЂжБЯпONКЭжБЯпACЕФНтЮіЪНГЩЗНГЬзщЃЌЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрЕуNЕФзјБъЮЊЃЈЉ3ЃЌ2ЃЉЃЎ
гжЁпЕуNЮЊЯпЖЮM1M2ЕФжаЕуЃЌ
ЁрЕуM2ЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЁрЕуMЕФзјБъЮЊЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮвЪаВшвЖзЈТєЕъЯњЪлФГЦЗХЦВшвЖЃЌЦфНјМлЮЊУПЧЇПЫ 240 дЊЃЌАДУПЧЇПЫ 400 дЊГіЪлЃЌЦНОљУПжмПЩЪлГі 200 ЧЇПЫЃЌКѓРДОЙ§ЪаГЁЕїВщЗЂЯжЃЌЕЅМлУПНЕЕЭ 10 дЊЃЌдђЦНОљУПжмЕФЯњЪлСППЩдіМг 40 ЧЇПЫЃЌШєИУзЈТєЕъЯњЪлетжжЦЗХЦВшвЖвЊЯыЦНОљУПжмЛёРћ 41600 дЊЃЌЧыЛиД№ЃК
ЃЈ1ЃЉУПЧЇПЫВшвЖгІНЕМлЖрЩйдЊЃП
ЃЈ2ЃЉдкЦНОљУПжмЛёРћВЛБфЕФЧщПіЯТЃЌЮЊОЁПЩФмШУРћгкЙЫПЭЃЌгЎЕУЪаГЁЃЌИУЕъгІАДдЪлМлЕФ МИелГіЪлЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
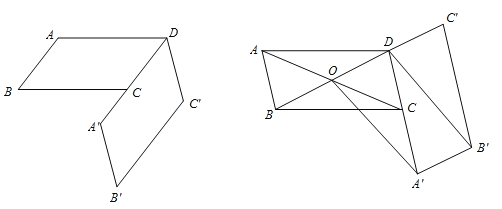
ЁОЬтФПЁПШчЭМЃЌвбжЊABCDЃЌAB=mЃЌAD=nЃЌНЋABCDШЦЕуDФцЪБеыа§зЊЃЌЕУЕНAЁЏBЁЏCDЃЌЕуAЁЏдкCDбгГЄЯпЩЯЃЎ
ЃЈ1ЃЉШєn=4ЃЌЕБBЁЏAЁЏЫљдкжБЯпЧЁКУОЙ§ЕуAЪБЃЌЧѓЕуAдЫЖЏЕНAЁЏЫљОЙ§ЕФТЗОЖЕФГЄЖШЃЛ
ЃЈ2ЃЉСЌНгACЁЂBDЯрНЛгкЕуOЃЌСЌНгOAЁЏЁЂDBЁЏЃЌЕБЫФБпаЮOAЁЏBЁЏDЮЊЦНааЫФБпаЮЪБЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
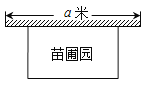
ЁОЬтФПЁПФГЕизМБИЮЇНЈвЛИіОиаЮУчЦддАЃЌЦфжавЛБпППЧНЃЌСэЭтШ§БпгУжмГЄЮЊ30УзЕФРщАЪЮЇГЩ.вбжЊЧНГЄЮЊ![]() УзЃЌЩшУчЦддАДЙжБгкЧНЕФвЛБпГЄЮЊ
УзЃЌЩшУчЦддАДЙжБгкЧНЕФвЛБпГЄЮЊ![]() УзЃЌУчЦддАЕФУцЛ§ЮЊ
УзЃЌУчЦддАЕФУцЛ§ЮЊ![]() ЦНЗНУз.
ЦНЗНУз.
ЃЈ1ЃЉжБНгаДГі![]() гы
гы![]() ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЕБ![]() ЪБЃЌЧѓ
ЪБЃЌЧѓ![]() ЕФзюДѓжЕ.
ЕФзюДѓжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
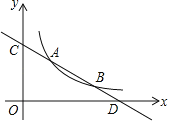
ЁОЬтФПЁПжБЯпyЃНkx+bгыЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЕФЭМЯѓЗжБ№НЛгкЕуAЃЈmЃЌ3ЃЉКЭЕуB ЃЈ6ЃЌnЃЉЃЌгызјБъжсЗжБ№НЛгкЕуCКЭЕу DЃЎ
ЃЈxЃО0ЃЉЕФЭМЯѓЗжБ№НЛгкЕуAЃЈmЃЌ3ЃЉКЭЕуB ЃЈ6ЃЌnЃЉЃЌгызјБъжсЗжБ№НЛгкЕуCКЭЕу DЃЎ
ЃЈ1ЃЉЧѓжБЯпABЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєЕуPЪЧxжсЩЯвЛЖЏЕуЃЌЕБSЁїADPЃН![]() SЁїBODЪБЃЌЧѓЕуPЕФзјБъЃЎ
SЁїBODЪБЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊе§ЗНаЮ![]() жаЃЌ
жаЃЌ![]() ЦНЗж
ЦНЗж![]() ЧвНЛ
ЧвНЛ![]() БпгкЕу
БпгкЕу![]() ЃЌНЋ
ЃЌНЋ![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊЕН
ЫГЪБеыа§зЊЕН![]() ЕФЮЛжУЃЌВЂбгГЄ
ЕФЮЛжУЃЌВЂбгГЄ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЎ
ЃЎ
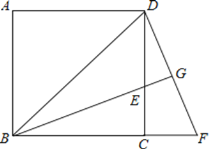
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎ
ЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌдкФГЬѕЙЋТЗЩЯгаAЃЌBЃЌCШ§ИіГЕеОЃЌвЛСОЦћГЕДгAеОвдЫйЖШv1дШЫйЪЛЯђBеОЃЌЕНДяBеОКѓВЛЭЃСєЃЌгжвдЫйЖШv2дШЫйЪЛЯђCеОЃЌЦћГЕааЪЛТЗГЬy(ЧЇУз)гыааЪЛЪБМфx(аЁЪБ)жЎМфЕФКЏЪ§ЭМЯѓШчЭМ2ЫљЪОЃЎ
(1)ЕБЦћГЕдкAЃЌBСНеОжЎМфдШЫйааЪЛЪБЃЌЧѓyгыxжЎМфЕФКЏЪ§ЙиЯЕЪНМАздБфСПЕФШЁжЕЗЖЮЇЃЛ
(2)ЕБЦћГЕЕФааЪЛТЗГЬЮЊ360ЧЇУзЪБЃЌЧѓДЫЪБЕФааЪЛЪБМфxЕФжЕЃЛ
(3)ШєЦћГЕдкФГвЛЖЮТЗГЬФкааЪЛСЫ90ЧЇУзгУЪБ50ЗжжгЃЌЧѓааЪЛЭъетЖЮТЗГЬЪБxЕФжЕЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГжжЩЬЦЗУПЬьЕФЯњЪлРћШѓyЃЈдЊЃЉгыЯњЪлЕЅМлxЃЈдЊЃЉжЎМфТњзуЙиЯЕЃКy=ax2+bxЉ75ЃЎЦфЭМЯѓШчЭМЃЎ
ЃЈ1ЃЉЯњЪлЕЅМлЮЊЖрЩйдЊЪБЃЌИУжжЩЬЦЗУПЬьЕФЯњЪлРћШѓзюДѓЃПзюДѓРћШѓЮЊЖрЩйдЊЃП
ЃЈ2ЃЉЯњЪлЕЅМлдкЪВУДЗЖЮЇЪБЃЌИУжжЩЬЦЗУПЬьЕФЯњЪлРћШѓВЛЕЭгк16дЊЃП

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ2ЕФе§ЗНаЮABCDжаЃЌEЃЌFЗжБ№ЮЊBCЁЂCDЕФжаЕуЃЌСЌНгAEЃЌBFНЛгкЕуGЃЌНЋЁїBCFбиBFЖделЃЌЕУЕНЁїBPFЃЌбгГЄFPНЛBAбгГЄЯпгкЕуQЃЌЯТСаНсТле§ШЗЖМгаЃЈЁЁЁЁЃЉИіЃЎ
ЂйQBЃНQFЃЛЂкAEЁЭBFЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЛЂмSЫФБпаЮECFGЃН2SЁїBGE
ЃЛЂмSЫФБпаЮECFGЃН2SЁїBGE

A.5B.4C.3D.2
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com