
����Ŀ����ͼ1����ij����·����A��B��C������վ��һ��������Aվ���ٶ�v1����ʻ��Bվ������Bվ��ͣ���������ٶ�v2����ʻ��Cվ��������ʻ·��y(ǧ��)����ʻʱ��x(Сʱ)֮��ĺ���ͼ����ͼ2��ʾ��
(1)��������A��B��վ֮��������ʻʱ����y��x֮��ĺ�����ϵʽ���Ա�����ȡֵ��Χ��
(2)����������ʻ·��Ϊ360ǧ��ʱ�����ʱ����ʻʱ��x��ֵ��
(3)��������ijһ��·������ʻ��90ǧ����ʱ50���ӣ�����ʻ�����·��ʱx��ֵ��

���𰸡���1��y��100x(0��x��3)����2��3.5����3��3![]()
��������
��1�������������ϵʽ������ͼ�����������ϵʽ���ٽ�y=300���룬���ɵó��𰸣�
��2�������ô���ϵ���������B��C�ĺ�����ϵʽ������y=360�����ɵó��𰸣�
��3����������0��x��3���ʱ�������ʻ��ʱ��ΪaСʱ���ٸ��������ͼ���г���a�ķ��̣����ȷ����ʻʱ�伴�ɵó��𰸣�
�⣺��1���赱������A��B��վ֮��������ʻʱ��y��x֮��ĺ�����ϵʽ��y��kx
��x=1ʱ��y=100=k��1,���k��100��
��y��100x��
��y��300ʱ��300��100x�����x��3��
�൱������A��B��վ֮��������ʻʱ��y��x֮��ĺ�����ϵʽ��y��100x(0��x��3)��
��2���赱3��x��4ʱ��y��x�ĺ�����ϵʽΪy��ax��b��
![]() ���
���![]()
�൱3��x��4ʱ��y��x�ĺ�����ϵʽΪy��120x��60��
��y��360ʱ��360��120x��60�����x��3.5��
�𣺵���������ʻ·��Ϊ360ǧ��ʱ����ʱ����ʻʱ��x��ֵ��3.5��
��3���ߵ�0��x��3ʱ��50����������ʻ��·��Ϊ(100��1)��![]() ��
��![]() ��
��![]() ��90��
��90��
��x��3ʱ��50����������ʻ��·��Ϊ[120��(4��3)]��![]() ��100��90��
��100��90��
����0��x��3���ʱ�������ʻ��ʱ��ΪaСʱ������3��x��4����ʻ��ʱ��Ϊ(![]() ��a)Сʱ��
��a)Сʱ��
(100��1)a��[120��(4��3)]��(![]() ��a)��90��
��a)��90��
���a��0.5��
��x��(3��0��5)��![]() ��
��![]() ��
��
��������ijһ��·������ʻ��90ǧ����ʱ50���ӣ���ʻ�����·��ʱx��ֵ��3![]() ��
��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=��x2+mx+m��2�Ķ���ΪA���Ҿ����㣨3����3��.
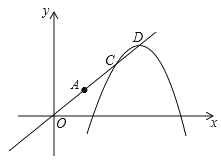
��1���������ߵĽ���ʽ������A������;
��2����ԭ������������OA�������ƽ�Ƶõ��µ������ߣ���������������OA����C��D���㣬��ͼ�����ʣ���������ƽ�ƵĹ����У��߶�CD�ij����Ƿ�Ϊ��ֵ�����ǣ�����������ֵ;�����ǣ���˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�������涨����������ҵ�������ɱ����ṩ��Ʒ����ѧ�����ۣ�������������ҵ����![]() ������
������![]() ������
������![]() �����ɱ���
�����ɱ���![]() ������
������![]() ��ѧ��С��Ͷ�����۱�����ҵ������һ�����ͽ��ܵƣ����鷢�֣�ÿ��������
��ѧ��С��Ͷ�����۱�����ҵ������һ�����ͽ��ܵƣ����鷢�֣�ÿ��������![]() ��
��![]() �����۵���
�����۵���![]() Ԫ
Ԫ![]() ֮��Ĺ�ϵ��������һ�κ�����
֮��Ĺ�ϵ��������һ�κ�����![]() ��֪���ֽ��ܵ�������Ϊÿ��12Ԫ�������������ɱ���Ϊÿ��mԪ
��֪���ֽ��ܵ�������Ϊÿ��12Ԫ�������������ɱ���Ϊÿ��mԪ![]()
��1����![]() ʱ��
ʱ��
������һ���µ����۵��۶�Ϊ20Ԫ�����һ��������Ҫ������ҵ��������Ԫ��
��������õ�����Ϊ![]() Ԫ
Ԫ![]() �������۵��۶�Ϊ����Ԫʱ��ÿ�¿ɻ���������
�������۵��۶�Ϊ����Ԫʱ��ÿ�¿ɻ���������
��2����۲��Ź涨�����ֽ��ܵƵ����۵��۲��ó���30Ԫ![]() ��������С�����Ӯ������ʱ����������ҵ������920Ԫ����m��x��������������m��ֵ��
��������С�����Ӯ������ʱ����������ҵ������920Ԫ����m��x��������������m��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
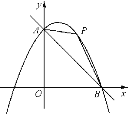
����Ŀ����ͼ��1����������y��ax2+6x+c��x����A��B���㣬��y���ڵ�C��ֱ��y��x+5������A��C��
��1���������ߵĽ���ʽ��
��2����ͼ��2����������B��ֱ�߽�ֱ��AC�ڵ�M��
����BM��ACʱ������������һ����P�������B��C�غϣ�����ֱ��BM��ƽ���߽�AC�ڵ�Q�����Ե�B��M��Q��PΪ������ı�����ƽ���ı��Σ����P�ĺ����ꣻ
������BC����ֱ��BM��ֱ��AC�ļнǵ��ڡ�ACB��2��ʱ����ֱ��д����M�����꣮
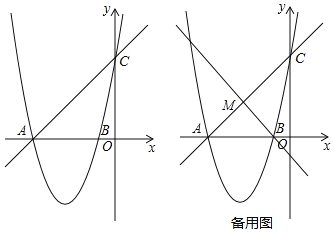
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��C����AOB��ƽ������һ�㣬��P��P���ֱ��ڱ�OA��OB�ϣ����Ҫ�õ� OP=OP������Ҫ�������������е�ijһ�����ɣ�����д�����п��ܵĽ�������Ϊ�� ��
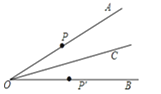
�١�OCP=��OCP�����ڡ�OPC=��OP��C����PC=P��C����PP���OC��
A.�٢�B.�ܢ�C.�٢ܢ�D.�٢ڢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ��ԭ��O��������ABCD�����ģ�����A��B������ֱ�Ϊ��1��1��������1��1������������ABCD��ԭ��O��ʱ����ת45���õ�������A��B��C��D������������ABCD��������A��B��C��D���ص������γɵ����˱��εı߳�Ϊ��������
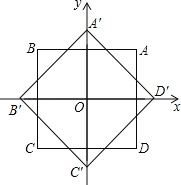
A.2��![]() B.2
B.2![]() ��2C.4��2
��2C.4��2![]() D.
D.![]() +1
+1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��m�dz�����
��m�dz�����
��1��֤��������mȡ��ֵʱ���ö��κ���ͼ������x�����������㣻
��2����![]() ��
��![]() �Ǹö��κ���ͼ���ϵ�������ͬ�㣬����κ�������ʽ��m��ֵ��
�Ǹö��κ���ͼ���ϵ�������ͬ�㣬����κ�������ʽ��m��ֵ��
��3����![]() ��
��![]() �ں���ͼ���ϣ���
�ں���ͼ���ϣ���![]() ����
����![]() ��ȡֵ��Χ��������ú�m��ʽ�ӱ�ʾ��.
��ȡֵ��Χ��������ú�m��ʽ�ӱ�ʾ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
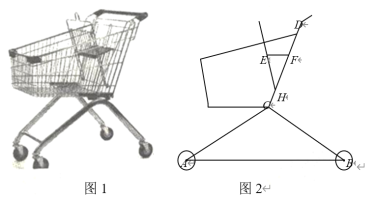
����Ŀ����ͼ1�dz��е����Ƴ�����ͼ2�������ʾ��ͼ����֪ǰ���ְ뾶��Ϊ5 cm���������ֵ�Բ�ĵ�����AB�����ƽ�У����֧��AC��BC��60cm��AC��CD����ֱ�������ļнǷֱ�Ϊ30����60����CD��50cm��
��1�������ǰ��D������ľ��룻
��2�����Ƴ���װ�м��ױ����Σ�EFΪС���壬�����ӵ�֧��H����C�ľ���Ϊ10 cm��DF��20cm��EF��AB����EHD��45����������EF�Ŀ��ȣ�������𰸾��������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() ��������
��������![]() ���ڵ�A��B����A��
���ڵ�A��B����A��![]() ���ϣ���B��
���ϣ���B��![]() ���ϣ�
���ϣ�
��1����������ߵĽ���ʽ��
��2����P��ֱ��AB�Ϸ����������ϵ�һ���㣬��S��AOB��S��PAB��8��3�����ʱ��P�����꣮
��3����E�������߶Գ����ϵĶ��㣬��F���������ϵĵ㣬�ж��м���λ���ܹ�ʹ�õ�E��F��B��OΪ������ı�����ƽ���ı��Σ�ֱ��д����Ӧ�ĵ�F�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com