
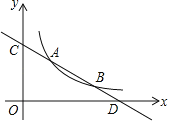
【题目】直线y=kx+b与反比例函数y=![]() (x>0)的图象分别交于点A(m,3)和点B (6,n),与坐标轴分别交于点C和点 D.
(x>0)的图象分别交于点A(m,3)和点B (6,n),与坐标轴分别交于点C和点 D.
(1)求直线AB的解析式;
(2)若点P是x轴上一动点,当S△ADP=![]() S△BOD时,求点P的坐标.
S△BOD时,求点P的坐标.
【答案】(1)y=﹣![]() x+4;(2)点P的坐标为(4,0)或(12,0).
x+4;(2)点P的坐标为(4,0)或(12,0).
【解析】
(1)先通过反比例函数解析式确定A(2,3),B(6,1),然后利用待定系数法求直线AB的解析式即可;
(2)先利用直线AB的解析式确定D(8,0),根据三角形面积公式计算出S△OBD=4,则S△ADP=6,设P(t,0),根据三角形面积公式得到![]() ×|t﹣8|×3=6,然后求出t即可得到点P的坐标.
×|t﹣8|×3=6,然后求出t即可得到点P的坐标.
解:(1)把点A(m,3)、B (6,n)分别代入y=![]() 得
得
3m=6,6n=6,
解得m=2,n=1,
∴A(2,3),B(6,1),
把A(2,3),B(6,1)代入y=kx+b,得
![]() ,
,
解得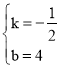 ,
,
∴直线AB的解析式为y=﹣![]() x+4;
x+4;
(2)连接OB
当y=0时,﹣![]() x+4=0,解得x=8,则D(8,0),
x+4=0,解得x=8,则D(8,0),
∵S△OBD=![]() ×8×1=4,
×8×1=4,
∴S△ADP=![]() S△BOD=6,
S△BOD=6,
设P(t,0),
∴![]() ×|t﹣8|×3=6,解得t=4或t=12,
×|t﹣8|×3=6,解得t=4或t=12,
∴点P的坐标为(4,0)或(12,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
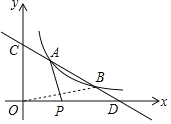
【题目】小亮将笔记本电脑水平放置在桌子上,显示屏OA与底板OB所在水平线的夹角为120°时,感觉最舒适(如图1),侧面示意图为图2;使用时为了散热,她在底板下面垫入散热架BCO'后,电脑转到B O′A′位置(如图3),侧面示意图为图4.已知OA=OB=28cm,O′C⊥OB于点C,O′C=14cm.
(参考数据:![]() ,
,![]() ,
,![]() )
)
(1)求∠CBO'的度数.
(2)显示屏的顶部A'比原来升高了多少cm?(结果精确到0.1cm)
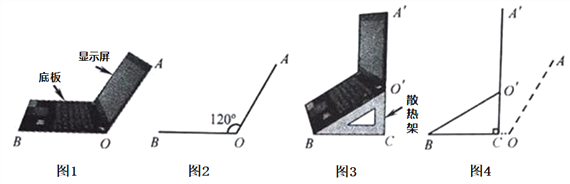
(3)如图4,垫入散热架后,要使显示屏O′A′与水平线的夹角仍保持120°,则显示屏O′A′应绕点O'按顺时针方向旋转多少度?(不写过程,只写结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
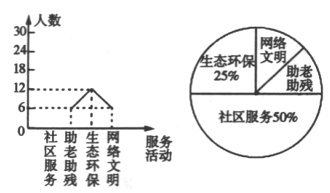
【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)求该班的人数;
(2)请把折线统计图补充完整;
(3)求扇形统计图中,网络文明部分对应的圆心角的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是⊙
是⊙![]() 的直径,
的直径,![]() 是⊙
是⊙![]() 上一点,
上一点,![]() 是
是![]() 的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连结AD.
的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连结AD.
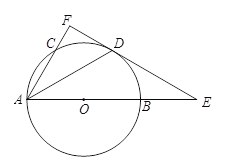
(1)求证:AF⊥EF; (2)若![]() ,AB=5,求线段BE的长.
,AB=5,求线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在 Rt△ABC 中,∠BAC=90°,AB=6,AC=8,D 为 AC 上一点,将△ABD 沿 BD 折叠,使点 A 恰好落在 BC 上的 E 处,则折痕 BD 的长是( )

A.5B.![]() C.3
C.3 ![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四个菱形①②③④的较小内角均与已知平行四边形ABCD的∠A相等,边长各不相同.将这四个菱形如图所示放入平行四边形中,未被四个菱形覆盖的部分用阴影表示.若已知两个阴影部分的周长的差,则不需测量就能知道周长的菱形为( )
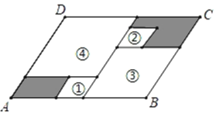
A.①B.②C.③D.④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
(1)求证:DE是⊙O的切线.
(2)求DE的长.
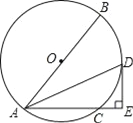
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D为AB的中点,以CD为直径的⊙O分别交AC,BC于点E,F两点,过点F作FG⊥AB于点G.
(1)试判断FG与⊙O的位置关系,并说明理由.
(2)若AC=3,CD=2.5,求FG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 交x轴于A、B两点,其中点A坐标为
交x轴于A、B两点,其中点A坐标为![]() ,与y轴交于点C,且对称轴在y轴的左侧,抛物线的顶点为P.
,与y轴交于点C,且对称轴在y轴的左侧,抛物线的顶点为P.
(1)当![]() 时,求抛物线的顶点坐标;
时,求抛物线的顶点坐标;
(2)当![]() 时,求b的值;
时,求b的值;
(3)在(1)的条件下,点Q为x轴下方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线![]() 、
、![]() 分别交抛物线的对称轴于点M、N.请问
分别交抛物线的对称轴于点M、N.请问![]() 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com