
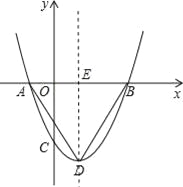
【题目】如图,二次函数y=ax2+bx+c(a>0)的图象的顶点为点D,其图象与x轴的交点A、B的横坐标分别为-1,3,与y轴负半轴交于点C.在下面五个结论中:①2a-b=0;②a+b+c>0;③c=-3a;④只有当a=![]() 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值有4个.其中正确的结论是________(只填序号).
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值有4个.其中正确的结论是________(只填序号).

【答案】③④
【解析】试题分析:先根据图象与x轴的交点A,B的横坐标分别为﹣1,3确定出AB的长及对称轴,再由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.①∵图象与x轴的交点A,B的横坐标分别为﹣1,3,∴AB=4,∴对称轴x=﹣![]() =1,即2a+b=0.故①错误;②根据图示知,当x=1时,y<0,即a+b+c<0.故②错误;③∵A点坐标为(﹣1,0),∴a﹣b+c=0,而b=﹣2a,∴a+2a+c=0,即c=﹣3a.故③正确;④∵△ADB为等腰直角三角形.所以AD=BD=
=1,即2a+b=0.故①错误;②根据图示知,当x=1时,y<0,即a+b+c<0.故②错误;③∵A点坐标为(﹣1,0),∴a﹣b+c=0,而b=﹣2a,∴a+2a+c=0,即c=﹣3a.故③正确;④∵△ADB为等腰直角三角形.所以AD=BD=![]() AB,设D(1,a+b+c),又b=﹣2a,c=﹣3a,故D(1,﹣4a);列方程求解得a=1/2或a=﹣1/2(舍去),∴只有a=1/2时三角形ABD为等腰直角三角形,故④正确;⑤要使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,当AB=BC=4时,∵AO=1,△BOC为直角三角形,又∵OC的长即为|c|,∴c2=16﹣9=7,∵由抛物线与y轴的交点在y轴的负半轴上,∴c=﹣
AB,设D(1,a+b+c),又b=﹣2a,c=﹣3a,故D(1,﹣4a);列方程求解得a=1/2或a=﹣1/2(舍去),∴只有a=1/2时三角形ABD为等腰直角三角形,故④正确;⑤要使△ACB为等腰三角形,则必须保证AB=BC=4或AB=AC=4或AC=BC,当AB=BC=4时,∵AO=1,△BOC为直角三角形,又∵OC的长即为|c|,∴c2=16﹣9=7,∵由抛物线与y轴的交点在y轴的负半轴上,∴c=﹣![]() ,与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=
,与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=![]() ;同理当AB=AC=4时,∵AO=1,△AOC为直角三角形,又∵OC的长即为|c|,∴c2=16﹣1=15,∵由抛物线与y轴的交点在y轴的负半轴上,∴c=﹣
;同理当AB=AC=4时,∵AO=1,△AOC为直角三角形,又∵OC的长即为|c|,∴c2=16﹣1=15,∵由抛物线与y轴的交点在y轴的负半轴上,∴c=﹣![]() 与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=
与2a+b=0、a﹣b+c=0联立组成解方程组,解得a=![]() ;同理当AC=BC时在△AOC中,AC2=1+c2,在△BOC中BC2=c2+9,∵AC=BC,∴1+c2=c2+9,此方程无解.经解方程组可知只有两个a值满足条件.故⑤错误.综上所述,正确的结论是③④.故答案是:③④.
;同理当AC=BC时在△AOC中,AC2=1+c2,在△BOC中BC2=c2+9,∵AC=BC,∴1+c2=c2+9,此方程无解.经解方程组可知只有两个a值满足条件.故⑤错误.综上所述,正确的结论是③④.故答案是:③④.


科目:初中数学 来源: 题型:
【题目】如图是药品研究所测得的某种新药在成人用药后,血液中的药物浓度y(微克/毫升)随用药后的时间x(小时)变化的图象(图象由线段OA与部分双曲线AB组成).并测得当y=a时,该药物才具有疗效.若成人用药4小时,药物开始产生疗效,且用药后9小时,药物仍具有疗效,则成人用药后,血液中药物浓度至少需要多长时间达到最大?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列式子中,计算正确的是( )
A. 2a2+2b2=2a2b2 B. 2a22b2=2a2b2 C. 2a23a3=6a5 D. 2a23a3=6a6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B、C三人玩篮球传球游戏,游戏规则是:第一次传球由A将球随机地传给B,C两人中的某一人,以后的每一次传球都是由上次的传球者随机地传给其他两人中的某一人.
(1)求两次传球后,球恰在B手中的概率;
(2)求三次传球后,球恰在A手中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=mx2-6x+1(m是常数).
(1)求证:不论m为何值,该函数的图象都经过y轴上的一个定点;
(2)若该函数的图象与x轴只有一个交点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在13×13的网格图中,已知△ABC和点M(1,2).
(1)以点M为位似中心,画出△ABC的位似图形△A′B′C′,其中△A′B′C′与△ABC的位似比为2;
(2)写出△A′B′C′的各顶点坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A. x3+x=2x4 B. a2a3=a6
C. (﹣2x2)3=﹣8x6 D. (x+3y)(x﹣3y)=x2﹣3y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016·泰安中考)如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=![]() 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.
(1)求反比例函数和一次函数的解析式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com