
【题目】如图,直线y![]() x+3分别与x轴,y轴交于点A、点B,抛物线y=x2+2x﹣2与y轴交于点C,点E在抛物线y=x2+2x﹣2的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )
x+3分别与x轴,y轴交于点A、点B,抛物线y=x2+2x﹣2与y轴交于点C,点E在抛物线y=x2+2x﹣2的对称轴上移动,点F在直线AB上移动,CE+EF的最小值是( )

A.4B.4.6C.5.2D.5.6
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如果三角形的两个内角α与β满足2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若△ABC是“准互余三角形”,∠C>90°,∠A=60°,则∠B= °;
(2)如图①,在Rt△ABC中,∠ACB=90°,AC=4,BC=5.若AD是∠BAC的平分线,不难证明△ABD是“准互余三角形”.试问在边BC上是否存在点E(异于点D),使得△ABE也是“准互余三角形”?若存在,请求出BE的长;若不存在,请说明理由.
(3)如图②,在四边形ABCD中,AB=7,CD=12,BD⊥CD,∠ABD=2∠BCD,且△ABC是“准互余三角形”,求对角线AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1=![]() 与一次函数y2=mx+n相交于A(﹣1,2),B(4,a)两点,AE⊥y轴于点E,则:
与一次函数y2=mx+n相交于A(﹣1,2),B(4,a)两点,AE⊥y轴于点E,则:
(1)求反比例函数与一次函数的解析式;
(2)若y1≤y2则直接写出x的取值范围;
(3)若M为反比例函数上第四象限内的一个动点,若满足S△ABM=S△AOB,则求点M的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用一条直线截三角形的两边,若所截得的四边形对角互补,则称该直线为三角形第三条边上的逆平行线.如图1,DE为△ABC的截线,截得四边形BCED,若∠BDE+∠C=180°,则称DE为△ABC边BC的逆平行线.如图2,已知△ABC中,AB=AC,过边AB上的点D作DE∥BC交AC于点E,过点E作边AB的逆平行线EF,交边BC于点F.
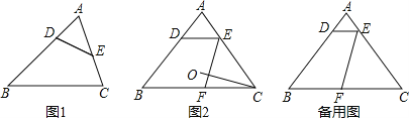
(1)求证:DE是边BC的逆平行线.
(2)点O是△ABC的外心,连接CO.求证:CO⊥FE.
(3)已知AB=5,BC=6,过点F作边AC的逆平行线FG,交边AB于点G.
①试探索AD为何值时,四边形AGFE的面积最大,并求出最大值;
②在①的条件下,比较AD+BG______AB大小关系.(“<、>或=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快城乡对接,建设全域美丽乡村,某地区对A、B两地间的公路进行改建.如图,A、B两地之间有一座山,汽车原来从A地到B地需途径C地沿折线ACB行驶,现开通隧道后,汽车可直接沿直线AB行驶.已知BC=80千米,∠A=45°,∠B=30°.
(1)开通隧道前,汽车从A地到B地大约要走多少千米?
(2)开通隧道后,汽车从A地到B地大约可以少走多少千米?(结果精确到0.1千米)(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,过点(﹣4,0),(0,﹣2).
(1)求抛物线的解析式和顶点坐标;
(2)当﹣4<x<4时,求y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节前夕举行了南通濠河国际龙舟邀请赛,在500米直道竞速赛道上,甲、乙两队所划行的路程y(单位:米)与时间t(单位:分)之间的函数关系式如图所示,根据图中提供的信息,有下列说法:①甲队比乙队提前0.5分到达终点②当划行1分钟时,甲队比乙队落后50米③当划行![]() 分钟时,甲队追上乙队④当甲队追上乙队时,两队划行的路程都是300米其中错误的是( )
分钟时,甲队追上乙队④当甲队追上乙队时,两队划行的路程都是300米其中错误的是( )
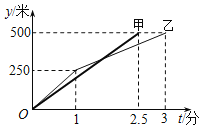
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
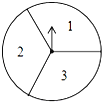
【题目】如图所示,可以自由转动的转盘被3等分,指针落在每个扇形内的机会均等.小明和小华利用这个转盘做游戏,若采用下列游戏规则:小明和小华各转一次,指针各指向一个数字,如果两数字之和是奇数是小明胜,否则小华胜。
(1)请用列表或画树状图的方法列出所有可能的情况;
(2)你认为这个游戏对双方公平吗?说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com