
【题目】如图,反比例函数y1=![]() 与一次函数y2=mx+n相交于A(﹣1,2),B(4,a)两点,AE⊥y轴于点E,则:
与一次函数y2=mx+n相交于A(﹣1,2),B(4,a)两点,AE⊥y轴于点E,则:
(1)求反比例函数与一次函数的解析式;
(2)若y1≤y2则直接写出x的取值范围;
(3)若M为反比例函数上第四象限内的一个动点,若满足S△ABM=S△AOB,则求点M的坐标.

【答案】(1)![]() ,
,![]() ;(2)x≤﹣1或0<x≤4;(3)点M的坐标(2,﹣1)或(3+
;(2)x≤﹣1或0<x≤4;(3)点M的坐标(2,﹣1)或(3+![]() ,
,![]() ).
).
【解析】
(1)先将点A代入反比例函数解析式中即可求出反比例函数的解析式,然后根据反比例函数的解析式求出点B的坐标,再利用待定系数法即可求出一次函数的解析式;
(2)根据图象及两个函数的交点即可得出x的取值范围;
(3)先求出一次函数与y轴的交点坐标,然后利用S△ABM=S△AOB和平移的相关知识分两种情况:向上平移或向下平移两种情况,分别求出平移后的直线与反比例函数在第四象限的交点即可.
(1)把A(﹣1,2)代入反比例函数![]() 得,k=﹣2
得,k=﹣2
∴反比例函数的关系式为![]() ,
,
把B(4,a)代入![]() 得,
得,![]() ,
,
∴B(4,![]() )
)
把A(﹣1,2),B(4,![]() )代入一次函数
)代入一次函数![]() 得,
得,
 解得
解得
∴一次函数的关系式为: ![]()
(2)当![]() 时,反比例函数的图象在一次函数图象的下方,
时,反比例函数的图象在一次函数图象的下方,
结合图象可知,当![]() ,自变量x的取值范围为:x≤﹣1或0<x≤4.
,自变量x的取值范围为:x≤﹣1或0<x≤4.
(3)当![]() 时,
时,![]()
∴![]() 与y轴的交点坐标为(0,
与y轴的交点坐标为(0,![]() ),如图:
),如图:

∵S△ABM=S△AOB
∴根据平行线间的距离处处相等,可将一次函数进行平移![]() 个单位,则平移后的直线与反比例函数在第四象限的交点即为所求的M点.
个单位,则平移后的直线与反比例函数在第四象限的交点即为所求的M点.
将![]() 向下平移
向下平移![]() 个单位过O点,关系式为:
个单位过O点,关系式为:![]() ,
,
 解得
解得 ,
,
∵M在第四象限,
∴M(2,﹣1),
将![]() 向上平移
向上平移![]() 个单位后直线的关系式为:
个单位后直线的关系式为:![]() ,
,
 解得
解得 ,
,
∵M在第四象限,
∴![]() ,
,
综上所述,点M的坐标(2,﹣1)或![]() ,
,


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】株洲五桥主桥主孔为拱梁钢构组合体系(如图1),小明暑假旅游时,来到五桥观光,发现拱梁的路面部分有均匀排列着9根支柱,他回家上网查到了拱梁是抛物线,其跨度为20米,拱高(中柱)10米,于是他建立如图2的坐标系,发现可以将余下的8根支柱的高度都算出来了,请你求出中柱左边第二根支柱CD的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC与△A′B′C′在平面直角坐标系中的位置如图.
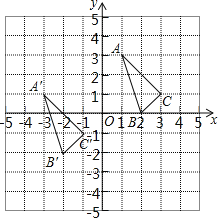
(1)分别写出下列各点的坐标: A′ ;B′ ;C′ ;
(2)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为 ;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读以下内容:
已知实数x,y满足x+y=2,且![]() 求k的值.
求k的值.
三位同学分别提出了以下三种不同的解题思路:
甲同学:先解关于x,y的方程组![]() ,再求k的值.
,再求k的值.
乙同学:先将方程组中的两个方程相加,再求k的值.
丙同学:先解方程组![]() ,再求k的值.
,再求k的值.
(2)你最欣赏(1)中的哪种思路?先根据你所选的思路解答此题,再对你选择的思路进行简要评价.
(评价参考建议:基于观察到题目的什么特征设计的相应思路,如何操作才能实现这些思路、运算的简洁性,以及你依此可以总结什么解题策略等等)
请先在以下相应方框内打勾,再解答相应题目.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若将一幅三角板按如图所示的方式放置,则下列结论中不正确的是( )

A. ∠1=∠3 B. 如果∠2=30°,则有AC∥DE
C. 如果∠2=30°,则有BC∥AD D. 如果∠2=30°,必有∠4=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校学生会向全校2900名学生发起了“爱心一日捐”捐款活动,为了解捐款情况,学生会随机调查了部分学生的捐款金额,并用得到的数据绘制了如下统计图①和图②,请根据相关信息,解答下列问题:
(Ⅰ)本次接受随机抽样调查的学生人数为 , 图①中m的值是;
(Ⅱ)求本次你调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校本次活动捐款金额为10元的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() (
(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,抛物线上的点
,抛物线上的点![]() 的横坐标为3,过点
的横坐标为3,过点![]() 作直线
作直线![]() 轴.
轴.
(1)点![]() 为抛物线上的动点,且在直线
为抛物线上的动点,且在直线![]() 的下方,点
的下方,点![]() ,
,![]() 分别为
分别为![]() 轴,直线
轴,直线![]() 上的动点,且
上的动点,且![]() 轴,当
轴,当![]() 面积最大时,求
面积最大时,求![]() 的最小值;
的最小值;
(2)过(1)中的点![]() 作
作![]() ,垂足为
,垂足为![]() ,且直线
,且直线![]() 与
与![]() 轴交于点
轴交于点![]() ,把
,把![]() 绕顶点
绕顶点![]() 旋转45°,得到
旋转45°,得到![]() ,再把
,再把![]() 沿直线
沿直线![]() 平移至
平移至![]() ,在平面上是否存在点
,在平面上是否存在点![]() ,使得以
,使得以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形为菱形?若存在直接写出点
为顶点的四边形为菱形?若存在直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
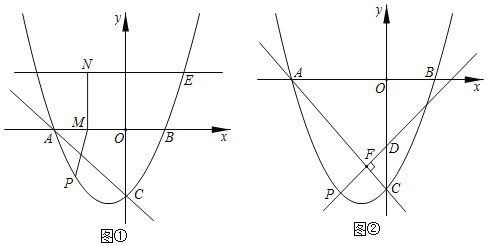
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题:二次根式与分式运算
(1)计算:( ![]() )﹣2+(
)﹣2+( ![]() ﹣
﹣ ![]() )0+(﹣1)1001+(
)0+(﹣1)1001+( ![]() ﹣3
﹣3 ![]() )×tan30°
)×tan30°
(2)先化简,再求值: ![]() ﹣
﹣ ![]() (
( ![]() ﹣a2+b2),其中a=3﹣2
﹣a2+b2),其中a=3﹣2 ![]() ,b=3
,b=3 ![]() ﹣3.
﹣3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生的爱国意识,某中学举办“爱我中华”朗诵比赛,全校学生都参加,并对表现优异的学生进行表彰,设置一、二、三等奖和进步奖共四个奖项,赛后,校统计小组随机抽取了九年级两个班级,并将这两个班的获奖情况绘制成以下两幅不完整的统计图.
请根据图中的信息,解答下列问题:
(1)求本次调查抽取的学生人数,并补全条形统计图;
(2)在扇形统计图中,表示“三等奖”的扇形所对应的圆心角度数是 72 °.
(3)若该校共有2600名学生,试估计得奖的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com