
����Ŀ����1���Ķ��������ݣ�
��֪ʵ��x��y����x+y=2����![]() ��k��ֵ��
��k��ֵ��
��λͬѧ�ֱ�������������ֲ�ͬ�Ľ���˼·��
��ͬѧ���Ƚ����x��y�ķ�����![]() ������k��ֵ��
������k��ֵ��
��ͬѧ���Ƚ��������е�����������ӣ�����k��ֵ��
��ͬѧ���Ƚⷽ����![]() ������k��ֵ��
������k��ֵ��
��2���������ͣ�1���е�����˼·���ȸ�������ѡ��˼·�����⣬�ٶ���ѡ���˼·���м�Ҫ���ۣ�
�����۲ο����飺���ڹ۲쵽��Ŀ��ʲô������Ƶ���Ӧ˼·����β�������ʵ����Щ˼·������ļ���ԣ��Լ������˿����ܽ�ʲô������Եȵȣ�
������������Ӧ�����ڴ��ٽ����Ӧ��Ŀ��
���𰸡��������ͣ�1���е���ͬѧ�Ľ���˼·��k=![]() ,���ۼ�����.
,���ۼ�����.
�����������������ѡ����ͬѧ�Ľ���˼·����+�ڵó�5x+5y=7k+4�����x+y=![]() =2����������𰸣�
=2����������𰸣�
���������
�������ͣ�1���е���ͬѧ�Ľ���˼·��
![]() ��
��
��+�ڵã�5x+5y=7k+4��
x+y=![]() ��
��
��x+y=2��
��![]() =2��
=2��
��ã�k=![]() ��
��
���ۣ���ͬѧ��ֱ�Ӹ��ݷ�����Ľ�ĸ����Ƚⷽ���飬�õ��ú�k��ʽ�ӱ�ʾx��y�ı���ʽ���ٴ���x+y=2�õ�����k�ķ��̣�û�о�������Ĺ۲��˼�����ⷨ�ȽϷ�������������
��ͬѧ�۲쵽�˷�������δ֪��x��y��ϵ�����Լ���x+y=2�е�ϵ���������ϵ���������������㣬���Ҳ������x��y��ֵ���ܽ�����⣬˼·�Ƚ���������С��
��ͬѧ������������Ϊһ�����壬���ɹ���x��y��k����Ԫһ�η����飬����ѡ���Ƚ�����ֻ��������δ֪��x��y�Ķ�Ԫһ�η����飬��Լ�������С����������ͬѧ�ļ�ࡢ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������x��ֱ���A��B���㣬����C��y�Ḻ�����ϣ�Ҳ��������ADEB�ı��ϣ���֪������ADEB�ı߳�Ϊ2����������FGMN�Ķ���F��G����x���ϣ�����M��N����ͼ�е��������ϣ���������FGMN�ı߳�Ϊ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������С��ÿ��С������ֱ����1��2��3��4��5����������е�һ������ЩС���������ֲ�ͬ���⣬�����ȫ����ͬ���ѷֱ��������4��5������С����벻���Ŀڴ� A �У��ѷֱ��������1��2��3������С����벻���Ŀڴ� B �У�������� A �� B �����ڴ��и�ȡ��һ��С�Ѵ� A �ڴ���ȡ����С���ϱ�����ּ��� m���� B �ڴ���ȡ����С���ϱ�����ּ���n����m��n=k�������x��һԪ���η���2x2��4x+k=0�н�ĸ����� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�D��BC���ϵ�һ�㣬E��AD���е㣬��A����BC��ƽ���߽�CE���ӳ����ڵ�F����AF��BD������BF��
��1����֤��BD��CD��
��2������ABC����ʲô����ʱ���ı���AFBD�Ǿ��Σ���˵�����ɣ�
��3���ڣ�2���������£��������AFBD�������Σ�ȷ����ABC����״��˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC����D�ǡ�ABC��һ�㣬AD=BD����AD��BD������CD������C��CE��BC��AD���ӳ����ڵ� E������BE������D��DF��CD��BC�ڵ�F��
��1����BD=DE= ![]() ��CE=
��CE= ![]() ����BC�ij���
����BC�ij���
��2����BD=DE����֤��BF=CF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������y1��![]() ��һ�κ���y2��mx+n�ཻ��A����1��2����B��4��a�����㣬AE��y���ڵ�E����
��һ�κ���y2��mx+n�ཻ��A����1��2����B��4��a�����㣬AE��y���ڵ�E����
��1������������һ�κ����Ľ���ʽ��
��2����y1��y2��ֱ��д��x��ȡֵ��Χ��
��3����MΪ�����������ϵ��������ڵ�һ�����㣬������S��ABM��S��AOB�������M�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��ȤС��ͬѧ���в�������CD�߶ȵ��ۺ�ʵ�������ͼ���ڵ�A�����ֱ���ڵ���Ĵ�������C������Ϊ36�㣬Ȼ������ͬһ�����б��AB����13�����¶�B����Ȼ������ˮƽ��������6���������ŵ�D����б��AB���¶ȣ����±ȣ�i=1��2.4����ô����CD�ĸ߶�ԼΪ���ο����ݣ�sin36���0.59��cos36���0.81��tan36���0.73���� ��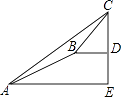
A.8.1��
B.17.2��
C.19.7��
D.25.5��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�CE��CF�ֱ�ƽ�֡�ACB�͡�ABC����ǡ�ACD��һ����O��AC���˶�������O��BD��ƽ�������ACB�͡�ACD�Ľ�ƽ���߷ֱ��ڵ�E�͵�F��
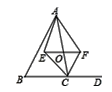
��1����֤������O�˶���ʲôλ��ʱ���ı���AECFΪ���Σ�˵�����ɣ�
��2���ڵڣ�1����Ļ����ϣ�����ABC����ʲô����ʱ���ı���AECFΪ�����Σ�˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com