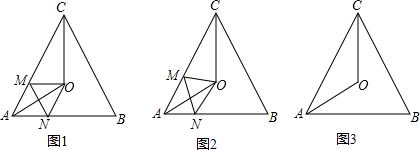
问题情境:已知,在等边△ABC中∠BAC与∠ACB的角平分线交于点O,点M、N分别在直线AC,AB上,且∠MON=60°请猜想CM、MN、AN三者之间的数量关系. 方法感悟:如图1,先将问题特殊化,当AM=AN,点M、N分别在边上时,CM、MN、AN三者之间的数量关系?
小芳的思考过程是:在线段MC上取一点D,构建全等三角形,可推出CM、MN、AN三者之间的数量关系;
小丽的思考过程是:在线段AB上取一点P,构建全等三角形,可推出CM、MN、AN三者之间的数量关系;
问题解决:(1)如图1已知:等边△ABC中,点O是边AC,BC的垂直平分线的交点,M,N分别在直线AC,BC上,且∠MON=60°.
(1)如图1,直接写出CM、MN、AN三者之间的数量关系;
(2)如图2,当AM≠AN时,M、N分别在边AC、BC上时,(1)中的结论是否仍然成立?若成立,请你加以证明;若不成立,请说明理由;
(3)当点M在边AC上,点N在BA的延长线上时,请你在图3中补全图形,标出相应字母,并直接写出线段CM、MN、AN三者之间的数量关系.