
【题目】如图,已知正方形ABCD的边长为12,BM=CN=5,CM,DN交于点O.则下列结论: 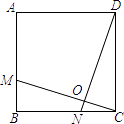
①DN⊥MC;②DN垂直平分MC;③sin∠OCD= ![]() ;④S△ODC=S四边形BMON中,
;④S△ODC=S四边形BMON中,
正确的有(填写序号)
【答案】①③④
【解析】解:∵四边形ABCD是正方形, ∴BC=CD,∠ABC=∠BCD=90°,
在△BMC和△CND中, ,
,
∴△BMC≌△CND,
∴∠MCB=∠NDC.
又∠MCN+∠MCD=90°,
∴∠MCD+∠NDC=90°,
∴∠DOC=90°,
∴DN⊥MC,故①正确;
在Rt△CDN中,∵CD=12,CN=5,
∴DN= ![]() =13.
=13.
又∵∠BCD=90°,∠COD=90°
∴ ![]() NCCD=
NCCD= ![]() NDOC,
NDOC,
∴OC= ![]() ,OM=13﹣
,OM=13﹣ ![]() =
= ![]() ,
,
∴OC≠OM,故②错误;
∵∠DNC+∠NDC=90°,∠ODC+∠OCD=90°,
∴∠OCD=∠DNC,
∴sin∠OCD=sin∠DNC= ![]() =
= ![]() ,故③正确;
,故③正确;
∵△BMC≌△CND,
∴S△BMC=S△CND
S△BMC﹣S△CNC=S△CND﹣S△CNC , 即S四边形BMON=S△ODC , 故④正确.
综上,正确的结论是①③④.
所以答案是①③④.
【考点精析】本题主要考查了勾股定理的概念和正方形的性质的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
【题目】某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,请根据图象回答下面的问题:

(1)出租车的起步价是多少元?当x>3时,求y关于x的函数关系式.
(2)若某乘客有一次乘出租车的车费为32元,求这位乘客乘车的里程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2﹣2x﹣3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.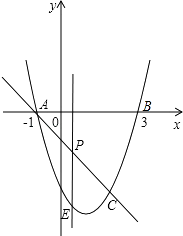
(1)求A、B两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,购买一种苹果,所付款金额y(元)与购买量x(千克)之间的函数图象由线段OA和射线AB组成,则一次购买5千克这种苹果比分五次购买1千克这种苹果可节省( )元.
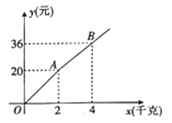
A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的五角星按一定的规律组成,其中第①个图形一共有2个五角星,第②个图形一共有8个五角星,第③个图形一共有18个五角星,…,则第⑥个图形中五角星的个数为( )
A.50
B.64
C.68
D.72
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一平面内四个点A,B,C,D.
(1)利用尺规,按下面的要求作图.要求:不写画法,保留作图痕迹,不必写结论.
①作射线AC;
②连接AB,BC,BD,线段BD与射线AC相交于点O;
③在线段AC上作一条线段CF,使CF=AC﹣BD.
(2)观察(1)题得到的图形,我们发现线段AB+BC>AC,得出这个结论的依据是 .
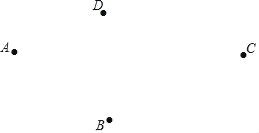
查看答案和解析>>
科目:初中数学 来源: 题型:
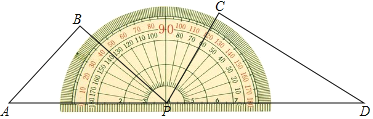
【题目】一副三角尺按如图所示摆放在量角器上,边PD与量角器0°刻度线重合,边AP与量角器180°刻度线重合,将三角尺ABP绕量角器中心点P以每秒4°的速度顺时针旋转,当边PB与0°刻度线重合时停止运动,设三角尺ABP的运动时间为t.
(1)当t=5时,边PB经过的量角器刻度线对应的度数是多少度;
(2)当t等于多少秒时,边PB平分∠CPD;
(3)若在三角尺ABP开始旋转的同时,三角尺PCD也绕点P以每秒1°的速度逆时针旋转,当三角尺ABP停止旋转时,三角尺PCD也停止旋转.
①当t为何值时,边PB平分∠CPD;
②在旋转过程中,是否存在某一时刻使∠BPD=2∠APC,若存在,请直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com