练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图是放在地面上的一个长方体盒子，其中，在线段的三等分点（E=3）处有一只蚂蚁，中点处有一米粒，则蚂蚁沿长方体表面爬到米粒处的最短距离为（ ）

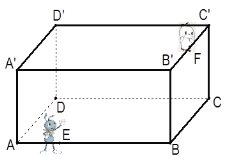
    A.10

    B.

    C.5+

    D.6+

    【答案】A

    【解析】

    利用平面展开图有两种情况，画出图形利用勾股定理求出EF的长即可．

    如图1，

    ∵AB=9,BB′=5,B′C′=6,在线段AB的三等分点E(靠近点A)处有一只蚂蚁,B′C′中点F处有一米粒，

    ∴BE=6，BF=5+3=8，

    ∴EF= =10；

    如图2,∵AB=9,BB′=5,B′C′=6,在线段AB的三等分点E(靠近点A)处有一只蚂蚁，

    B′C′中点F处有一米粒，

    ∴BE=6，EN=9，FN=5，

    ∴EF= .

    ∵10<，

    ∴蚂蚁沿长方体表面爬到米粒处的最短距离为10.

    故选A.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

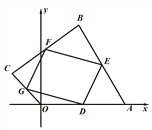
    【题目】如图，在平面直角坐标系xOy中，四边形OABC的顶点A在x轴的正半轴上，OA=4，OC=2，点D、E、F、G分别为边OA、AB、BC、CO的中点，连结DE、EF、FG、GD.

    （1）若点C在y轴的正半轴上，当点B的坐标为（2，4）时，判断四边形DEFG的形状，并说明理由.

    （2）若点C在第二象限运动，且四边形DEFG为菱形时，求点四边形OABC对角线OB长度的取值范围.

    （3）若在点C的运动过程中，四边形DEFG始终为正方形，当点C从X轴负半轴经过Y轴正半轴，运动至X轴正半轴时，直接写出点B的运动路径长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】鸡兔同笼问题是我国古代著名趣题之一，大约在 1500 年前，《孙子算经》中就记载了这个有趣的问题．书中是这样叙述的：“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？”这四句话的意思是：有若干只鸡、兔同在一个笼子里，从上上面数，有 35 个头；从下面数，有 94 只脚 ．求笼中各有几只鸡和兔？经计算可得（ ）

    A. 鸡 20 只，兔 15 只 B. 鸡 12 只，兔 23 只

    C. 鸡 15 只，兔 20 只 D. 鸡 23 只，兔 12 只

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知多项式，次数是b，3a与b互为相反数，在数轴上，点A表示数a，点B表示数b．

    数轴上A、B之间的距离记作，定义：设点C在数轴上对应的数为x，当时，直接写出x的值．

    有一动点P从点A出发第一次向左运动1个单位长度，然后在新的位置第二次运动，向右运动2个单位长度，在此位置第三次运动，向左运动3个单位长度按照如此规律不断地左右运动，当运动了2019次时，求点P所对应的有理数．

    若小蚂蚁甲从点A处以1个单位长度秒的速度向左运动，同时小蚂蚁乙从点B处以2单位长度秒的速度也向左运动，一同学观察两只小蚂蚁运动，在它们刚开始运动时，在原点O处放置一颗饭粒，乙在碰到饭粒后立即背着饭粒以原来的速度向相反的方向运动，设运动的时间为t秒，求甲、乙两只小蚂蚁到原点的距离相等时所对应的时间t．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A、B和线段MN都在数轴上，点A、M、N、B对应的数字分别为﹣1、0、2、11．线段MN沿数轴的正方向以每秒1个单位的速度移动，移动时间为t秒．

    （1）用含有t的代数式表示AM的长为　　

    （2）当t=　　秒时，AM+BN=11．

    （3）若点A、B与线段MN同时移动，点A以每秒2个单位速度向数轴的正方向移动，点B以每秒1个单位的速度向数轴的负方向移动，在移动过程，AM和BN可能相等吗？若相等，请求出t的值，若不相等，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB、CD相交于点O，OE平分∠BOD，OF平分∠COE．

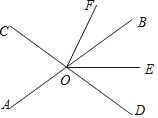
    （1）若∠AOC=76°，求∠BOF的度数；

    （2）若∠BOF=36°，求∠AOC的度数；

    （3）若|∠AOC﹣∠BOF|=α°，请直接写出∠AOC和∠BOF的度数．（用含的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

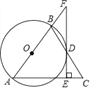
    【题目】如图，在△ABC中，AB=AC，以AB为直径的⊙O与边BC交于点D，DE⊥AC，垂足为E，交AB的延长线于点F．

    （1）求证：EF是⊙O的切线；

    （2）若∠C=60°，AC=12，求的长．

    （3）若tanC=2，AE=8，求BF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（10分）如图，AB为⊙O的直径，直线CD切⊙O于点D，AM⊥CD于点M，BN⊥CD于N．

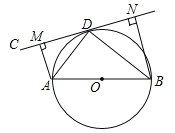
    （1）求证：∠ADC=∠ABD；

    （2）求证：AD2=AMAB；

    （3）若AM=，sin∠ABD=，求线段BN的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，等腰直角三角形ABC位于第一象限，AB=AC=2，直角顶点A在直线y=x上，其中A点的横坐标为1，且两条直角边AB、AC分别平行于x轴、y轴，若双曲线(k≠0)与△ABC有交点，则k的取值范围是（ ）

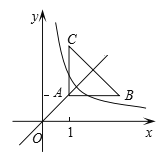
    A. 1≤k≤4 B. 1≤k＜4 C. 1＜k＜2 D. 1≤k≤3

    查看答案和解析>>

    同步练习册答案