
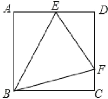
【题目】如图,正方形 ABCD 的边长为 2,点 E,F 分别在边AD,CD 上,若EBF 45 ,则EDF 的周长等于_____.
【答案】4
【解析】
根据正方形的性质得AB=BC,∠BAE=∠C=90°,根据旋转的定义,把△ABE绕点B顺时针旋转90°可得到△BCG,根据旋转的性质得BG=BE,CG=AE,∠GBE=90°,∠BAE=∠C=90°,∠EBG=∠ABC=90°,于是可判断点G在CB的延长线上,接着利用“SAS”证明△FBG≌△EBF,得到EF=CF+AE,然后利用三角形周长的定义得到答案.
解:∵四边形ABCD为正方形,
∴AB=BC,∠BAE=∠BCD=90°,
∴把△ABE绕点B顺时针旋转90°可得到△BCG,如图,
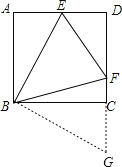
∴BG=BE,CG=AE,∠GBE=90°,∠BAE=∠BCG=90°,
∴点G在DC的延长线上,
∵∠EBF=45°,
∴∠FBG=∠EBG-∠EBF=45°,
∴∠FBG=∠FBE,
在△FBG和△EBF中,
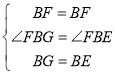 ,
,
∴△FBG≌△FBE(SAS),
∴FG=EF,
而FG=FC+CG=CF+AE,
∴EF=CF+AE,
∴△DEF的周长=DF+DE+CF+AE=CD+AD=2+2=4
故答案为:4.


科目:初中数学 来源: 题型:
【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元) | 180 | 260 | 280 | 300 |
y(间) | 100 | 60 | 50 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每间空置的客房,宾馆每日需支出各种费用60元.当房价为多少元时,宾馆当日利润最大?求出最大利润.(宾馆当日利润=当日房费收入-当日支出)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是( )

A.90°B.80°C.50°D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别站在相距 6 米的 A , B 两点练习打羽毛球,已知羽毛球飞行的路线为抛物线的一部分,甲在离地面 1 米的C 处发出一球,乙在离地面 1.5 米的 D 处成功击球,球飞行过程中的最高点 H 与甲的水平距离 AE 为 4 米,现以 A 为原点,直线 AB 为 x 轴, 建立平面直角坐标系(如图所示).
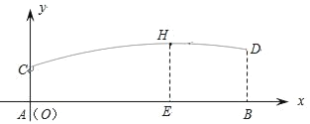
(1)求羽毛球飞行的路线所在的抛物线的表达式;
(2)求羽毛球飞行的最高高度。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与一次函数
与一次函数![]() ,令W=
,令W=![]() .
.
(1)若![]() 、
、![]() 的函数图像交于x轴上的同一点.
的函数图像交于x轴上的同一点.
①求![]() 的值;
的值;
②当![]() 为何值时,W的值最小,试求出该最小值;
为何值时,W的值最小,试求出该最小值;
(2)当![]() 时,W随x的增大而减小.
时,W随x的增大而减小.
①求![]() 的取值范围;
的取值范围;
②求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
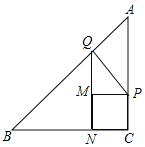
【题目】如图,在Rt![]() ABC中,∠C=90°,AC=BC=4cm,动点P从点C出发以1cm/s的速度沿CA匀速运动,同时动点Q从点A出发以
ABC中,∠C=90°,AC=BC=4cm,动点P从点C出发以1cm/s的速度沿CA匀速运动,同时动点Q从点A出发以![]() 的速度沿AB匀速运动,当点P到达点A时,点P、Q同时停止运动,设运动时间为他t(s).
的速度沿AB匀速运动,当点P到达点A时,点P、Q同时停止运动,设运动时间为他t(s).
(1)当t为何值时,点B在线段PQ的垂直平分线上?
(2)是否存在某一时刻t,使![]() APQ是以PQ为腰的等腰三角形?若存在,求出
APQ是以PQ为腰的等腰三角形?若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(3)以PC为边,往CB方向作正方形CPMN,设四边形QNCP的面积为S,求S关于t的函数关系式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com