
【题目】已知x,x是关于x的一元二次方程x2+(2m+1)x+m2+1=0的两个实数根,
①求m取值范围;
②若x12+x22=15,求实数m的值;
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】如图,分别以直角![]() 的斜边AB,直角边AC为边向
的斜边AB,直角边AC为边向![]() 外作等边
外作等边![]() 和等边
和等边![]() ,F为AB的中点,DE与AB交于点G,EF与AC交于点H,
,F为AB的中点,DE与AB交于点G,EF与AC交于点H,![]() ,
,![]() .给出如下结论:
.给出如下结论:
①EF⊥AC; ②四边形ADFE为菱形; ③![]() ; ④
; ④![]() ;
;
其中正确结论的是( )

A. ①②③B. ②③④C. ①③④D. ①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某新型高科技商品,每件的售价比进价多6元,5件的进价相当于4件的售价,每天可售出200件,经市场调查发现,如果每件商品涨价1元,每天就会少卖5件.
(1)该商品的售价和进价分别是多少元?
(2)设每天的销售利润为w元,每件商品涨价x元,则当售价为多少元时,该商品每天的销售利润最大,最大利润为多少元?
(3)为增加销售利润,营销部推出了以下两种销售方案:方案一:每件商品涨价不超过8元;方案二:每件商品的利润至少为24元,请比较哪种方案的销售利润更高,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.阜阳市某家快递公司,2017年3月份与5月份完成投递的快递总件数分别为10万件和12.1万件.现假定该公司每月投递的快递总件数的增长率相同.
(1)求该快递公司投递快递总件数的月平均增长率?
(2) 如果平均每人每月最多可投递快递0.6万件,那么该公司现有的21名快递投递业务员能否完成2017年6月份的快递投递任务?如果不能,请问至少需要增加几名业务员?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=BC,AB=8,点D为AB的中点,若直角MDN绕点D旋转,分别交AC于点E,交BC于F,则下列说法:①AE=CF;②EC+CF=4![]() ;③DE=DF;④若△ECF面积为一个定值,则EF长也是一个定值,其中正确的结论是_____.
;③DE=DF;④若△ECF面积为一个定值,则EF长也是一个定值,其中正确的结论是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1,已知抛物线 y ax![]() bx c 经过 A3,0,B 1,0 ,C 0,3 三点,其顶点为D,对称轴是直线l , l 与 x 轴交于点 H .
bx c 经过 A3,0,B 1,0 ,C 0,3 三点,其顶点为D,对称轴是直线l , l 与 x 轴交于点 H .
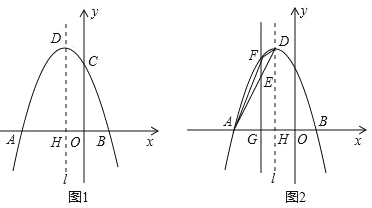
(1)求该抛物线的解析式;
(2)若点 P 是该抛物线对称轴l 上的一个动点,求PBC 周长的最小值;
(3)如图 2,若 E 是线段 AD 上的一个动点( E 与 A, D 不重合),过 E 点作平行于 y 轴的直线交抛物线于点 F ,交 x 轴于点G ,设点 E 的横坐标为m ,四边形 AODF 的面积为 S 。
①求 S 与 m 的函数关系式;
② S 是否存在最大值,若存在,求出最大值及此时点 E 的坐标,若不存在,请说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2014年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套,设销售单价为x(x60)元,销售量为y套.
(1)求出y与x的函数关系式;
(2)当销售单价为多少元时,且销售额为14000元?
(3)当销售单价为多少元时,才能在一个月内获得最大利润,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com