
【题目】甲、乙两人分别站在相距 6 米的 A , B 两点练习打羽毛球,已知羽毛球飞行的路线为抛物线的一部分,甲在离地面 1 米的C 处发出一球,乙在离地面 1.5 米的 D 处成功击球,球飞行过程中的最高点 H 与甲的水平距离 AE 为 4 米,现以 A 为原点,直线 AB 为 x 轴, 建立平面直角坐标系(如图所示).
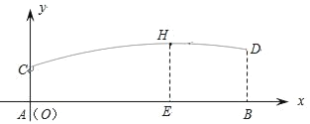
(1)求羽毛球飞行的路线所在的抛物线的表达式;
(2)求羽毛球飞行的最高高度。
科目:初中数学 来源: 题型:
【题目】如图1,抛物线![]() 与x轴交于A、B两点(A在B的左侧),与y轴正半轴交于点C,抛物线的顶点为P,对称轴为直线
与x轴交于A、B两点(A在B的左侧),与y轴正半轴交于点C,抛物线的顶点为P,对称轴为直线![]() ,且OC=3OA.
,且OC=3OA.
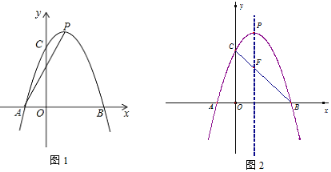
(1)求抛物线的解析式;
(2)点D(2,m)在抛物线上,点E在直线AP上,使DE⊥OE,求点E的横坐标;
(3)如图2,连接BC与抛物线的对称轴交于点F,在抛物线上是否存在点G,使△GPF与△GBF的面积相等,若存在,求出点G坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批 30 瓦的 LED 灯泡和普通白炽灯泡进行销售,其进价与标价如下表:
LED 灯泡 | 普通白炽灯泡 | |
进价(元) | 45 | 25 |
标价(元) | 60 | 30 |

(1)该商场购进了 LED 灯泡与普通白炽灯泡共 300 个,LED 灯泡按标价进行销售,而普通 白炽灯泡打九折销售,当销售完这批灯泡后可获利 3 200 元,求该商场购进 LED 灯泡与 普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进这两种灯泡 120 个, 在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的 30%, 并求出此时这批灯泡的总利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,我国政府为减轻农民负担,决定在5年内免去农业税.某乡今年人均上缴农业税25元,若两年后人均上缴农业税为16元,假设这两年降低的百分率相同.
(1)求降低的百分率;
(2)若小红家有4人,明年小红家减少多少农业税?
查看答案和解析>>
科目:初中数学 来源: 题型:
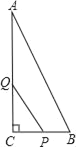
【题目】如图,△ABC中,∠C=90°,AC=16cm,BC=8cm,一动点P从点C出发沿着CB方向以2cm/s的速度运动,另一动点Q从A出发沿着AC边以4cm/s的速度运动,P、Q两点同时出发,运动时间为t(s).
(1)若△PCQ的面积是△ABC面积的![]() ,求t的值?
,求t的值?
(2)△PCQ的面积能否与四边形ABPQ面积相等?若能,求出t的值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,
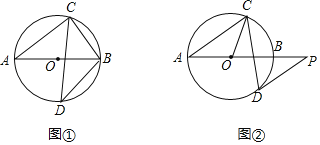
(1)如图①,若D为弧AB的中点,求∠ABC和∠ABD的大小;
(2)如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
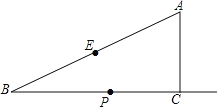
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]()
(1)通过配方将它写成![]() 的形式.
的形式.
(2)当![]() 时,函数有最 值,是 .
时,函数有最 值,是 .
(3)当![]() 时,
时,![]() 随
随![]() 的增大而增大;)当
的增大而增大;)当![]() 时,
时,![]() 随
随![]() 的增大而减小.
的增大而减小.
(4)该函数图象由![]() 的图象经过怎样的平移得到?
的图象经过怎样的平移得到?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com