
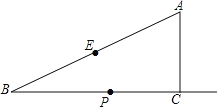
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为_____.
【答案】2或2![]()
【解析】
根据30°角所对的直角边等于斜边的一半可求出AB,即可得到AE的值,然后根据勾股定理求出BC.①若PA'与AB交于点F,连接A'B,如图1,易得S△EFP![]() S△BEP
S△BEP![]() S△A'EP,即可得到EF
S△A'EP,即可得到EF![]() BE=BF,PF
BE=BF,PF![]() A'P=A'F.从而可得四边形A'EPB是平行四边形,即可得到BP=A'E,从而可求出BP;②若EA'与BC交于点G,连接AA',交EP与H,如图2,同理可得GP=BG,EG
A'P=A'F.从而可得四边形A'EPB是平行四边形,即可得到BP=A'E,从而可求出BP;②若EA'与BC交于点G,连接AA',交EP与H,如图2,同理可得GP=BG,EG![]() EA'=1,根据三角形中位线定理可得AP=2=AC,此时点P与点C重合(BP=BC),从而可求出BP.
EA'=1,根据三角形中位线定理可得AP=2=AC,此时点P与点C重合(BP=BC),从而可求出BP.
∵∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,
∴AB=4,AE![]() AB=2,BC=2
AB=2,BC=2![]() .
.
①若PA'与AB交于点F,连接A'B,如图1.

由折叠可得S△A'EP=S△AEP,A'E=AE=2.
∵点E是AB的中点,
∴S△BEP=S△AEP![]() S△ABP.
S△ABP.
由题可得S△EFP![]() S△ABP,
S△ABP,
∴S△EFP![]() S△BEP
S△BEP![]() S△AEP
S△AEP![]() S△A'EP,
S△A'EP,
∴EF![]() BE=BF,PF
BE=BF,PF![]() A'P=A'F,
A'P=A'F,
∴四边形A'EPB是平行四边形,
∴BP=A'E=2;
②若EA'与BC交于点G,连接AA',交EP与H,如图2.
 .
.
同理可得GP![]() BP=BG,EG
BP=BG,EG![]() EA'
EA'![]() 2=1.
2=1.
∵BE=AE,
∴EG![]() AP=1,
AP=1,
∴AP=2=AC,
∴点P与点C重合,
∴BP=BC=2![]() .
.
故答案为:2或2![]() .
.


科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c开口向上,与x轴交于点A、B,与y轴交于点C

(1) 如图1,若A (1,0)、C (0,3)且对称轴为直线x=2,求抛物线的解析式
(2) 在(1)的条件下,如图2,作点C关于抛物线对称轴的对称点D,连接AD、BD,在抛物线上是否存在点P,使∠PAD=∠ADB,若存在,求出点P的坐标,若不存在,请说明理由
(3) 若直线l:y=mx+n与抛物线有两个交点M、N(M在N的左边),Q为抛物线上一点(不与M、N重合),过点Q作QH平行于y轴交直线l于点H,求![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别站在相距 6 米的 A , B 两点练习打羽毛球,已知羽毛球飞行的路线为抛物线的一部分,甲在离地面 1 米的C 处发出一球,乙在离地面 1.5 米的 D 处成功击球,球飞行过程中的最高点 H 与甲的水平距离 AE 为 4 米,现以 A 为原点,直线 AB 为 x 轴, 建立平面直角坐标系(如图所示).
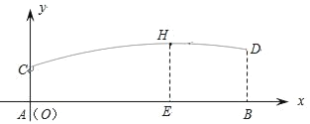
(1)求羽毛球飞行的路线所在的抛物线的表达式;
(2)求羽毛球飞行的最高高度。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 中,
中,![]() ,点
,点![]() 是
是![]() 内一点,连接
内一点,连接![]() ,且
,且![]() ,设
,设![]() .
.
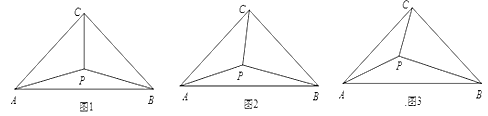
(1)如图1,若![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,连结
,连结![]() ,易证
,易证![]() 为等边三角形,则
为等边三角形,则![]() ,
,![]() ;
;
(2)如图2,若![]() ,则
,则![]() ,
,![]() ;
;
(3)如图3,试猜想![]() 和
和![]() 之间的数量关系,并给予证明.
之间的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与一次函数
与一次函数![]() ,令W=
,令W=![]() .
.
(1)若![]() 、
、![]() 的函数图像交于x轴上的同一点.
的函数图像交于x轴上的同一点.
①求![]() 的值;
的值;
②当![]() 为何值时,W的值最小,试求出该最小值;
为何值时,W的值最小,试求出该最小值;
(2)当![]() 时,W随x的增大而减小.
时,W随x的增大而减小.
①求![]() 的取值范围;
的取值范围;
②求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011山东济南,27,9分)如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线![]() 经过A、C两点,与AB边交于点D.
经过A、C两点,与AB边交于点D.
(1)求抛物线的函数表达式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线![]() 的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.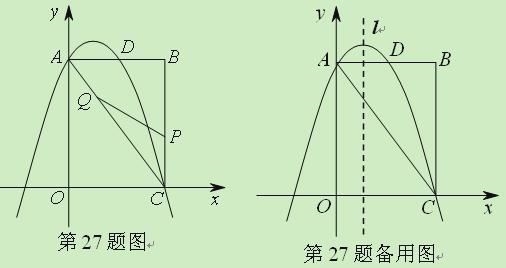
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】形如![]() 的函数称为反比例函数,我们定义,如果一次函数
的函数称为反比例函数,我们定义,如果一次函数![]() 和反比例函数
和反比例函数![]() 的系数a、b、c(abc≠0)满足
的系数a、b、c(abc≠0)满足![]() ,则称二次函数
,则称二次函数![]() 为一次函数函数y1和反比例函数y2的“调和二次函数”.
为一次函数函数y1和反比例函数y2的“调和二次函数”.
(1)试判断一次函数![]() 反比例函数
反比例函数![]() 的“调和二次函数”是否存在,并说明理;
的“调和二次函数”是否存在,并说明理;
(2)若二次函数 y3 m 1 x2 2mx 4 是某一次函数和反比例函数的“调和二次函数”,试求该一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
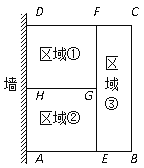
【题目】为了节省材料,某养殖户利用墙 (墙足够长)为一边,用总长为80m的篱笆围成了如图所示的①②③三块矩形区域养鸡场,而且这三块矩形区域的面积相等.若矩形区域ABCD的面积为300m2.求BC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自从湖南与欧洲的“湘欧快线”开通后,我省与欧洲各国经贸往来日益频繁,某欧洲客商准备在湖南采购一批特色商品,经调查,用16 000元采购A型商品的件数是用7 500元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多10元.
(1)求一件A,B型商品的进价分别为多少元?
(2)若该欧洲客商购进A,B型商品共250件进行试销,其中A型商品的件数不大于B型的件数,且不小于80件,已知A型商品的售价为240元/件,B型商品的售价为220元/件,且全部售出.设购进A型商品m件,求该客商销售这批商品的利润v与m之间的函数解析式,并写出m的取值范围;
(3)在(2)的条件下,欧洲客商决定在试销活动中每售出一件A型商品,就从一件A型商品的利润中捐献慈善资金a元,求该客商售完所有商品并捐献慈善资金后获得的最大收益.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com