
【题目】如图,在等腰![]() 中,
中,![]() ,点
,点![]() 是
是![]() 内一点,连接
内一点,连接![]() ,且
,且![]() ,设
,设![]() .
.
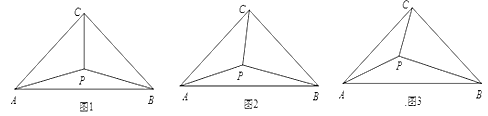
(1)如图1,若![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,连结
,连结![]() ,易证
,易证![]() 为等边三角形,则
为等边三角形,则![]() ,
,![]() ;
;
(2)如图2,若![]() ,则
,则![]() ,
,![]() ;
;
(3)如图3,试猜想![]() 和
和![]() 之间的数量关系,并给予证明.
之间的数量关系,并给予证明.
【答案】(1)![]() ,
,![]() (2)
(2)![]() ,
,![]() (3)
(3)![]()
【解析】
(1)将△PBC绕点C顺时针旋转90°至△DAC,连结DP,只要证明△DAP为等边三角形,即可解决问题;
(2)将△PBC绕点C顺时针旋转90°至△DAC,连结DP,只要证明△DAP为等腰直角三角形,即可解决问题;
(3)将△PBC绕点C顺时针旋转90°至△DAC,连结DP,只要证明△BPA≌△BPD(SSS),即可解决问题;
解:(1)如图1中,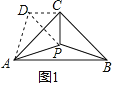
由旋转不变性可知:![]() ,
,![]() ,
,![]() ,
,
∵在等腰![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,CP为三线合一的线
,CP为三线合一的线
∴![]() ,
,![]()
∴![]()
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() 为等腰直角三角形
为等腰直角三角形
∴![]() ,
,
∴![]() ,
,
∴△APD是等边三角形,
∴∠ADP=∠APD=60°,
∵∠CDP=∠CPD=45°,
∴∠ADC=∠APC=∠CPB=105°,
∴∠APB=360°-105°-105°=150°,
∴α=150°,β=105°,
故答案为150°,105°.
(2)将△PBC绕点C顺时针旋转90°至△DAC,连结DP.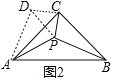
由旋转不变性可知:BP=AD,CD=CP,∠DCP=90°,
∴![]() 为等腰直角三角形
为等腰直角三角形
∴![]() ,
,
∵![]() ,
,
![]() ,
,
∴![]() ,
,![]() ,
,
∴△ADP是等腰直角三角形,
∴∠APD=90°,∠ADP=45°,
∴∠APC=135°,∠BPC=∠ADC=90°,
∴∠APB=360°-135°-90°=135°,
∴α=135°,β=90°,
故答案为135°,90°.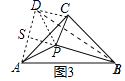
(3)将△PBC绕点C顺时针旋转90°至△DAC,连结DP,延长PB交AD与S,
由旋转不变性可知:BP=AD,CD=CP,∠DCP=90°,
∴![]() 为等腰直角三角形
为等腰直角三角形
∴![]() ,
,
∵![]() ,
,
∴PA=PD,
∵∠BPC+∠CPS=180°,∠BPC=∠ADC,
∴∠ADC+∠CPS=180°,
∴∠PSD+∠PCD=180°,
∴∠PSD=90°,
∴PS⊥AD,
∵PA=PD,
∴△ADP是等腰直角三角形,
∴SA=SD,
∴△ABP是等腰直角三角形,
∴BA=BD,
∵BP=BP,PA=PD,BA=BD,
∴△BPA≌△BPD(SSS),
∴∠APB=∠BPD,
∴![]() ∠BPD-∠BPC=∠CPD=45°,
∠BPD-∠BPC=∠CPD=45°,
即:![]() .
.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案科目:初中数学 来源: 题型:
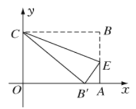
【题目】如图,在平面直角坐标系中放入一个一边长OC为9的矩形纸片ABCO,将纸片翻折后,点B恰好落在x轴上,记为点B′,折痕为CE,已知tan∠OB′C=![]() .
.
(1)求点B′的坐标;
(2)求折痕CE所在直线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年,我国政府为减轻农民负担,决定在5年内免去农业税.某乡今年人均上缴农业税25元,若两年后人均上缴农业税为16元,假设这两年降低的百分率相同.
(1)求降低的百分率;
(2)若小红家有4人,明年小红家减少多少农业税?
查看答案和解析>>
科目:初中数学 来源: 题型:
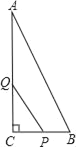
【题目】如图,△ABC中,∠C=90°,AC=16cm,BC=8cm,一动点P从点C出发沿着CB方向以2cm/s的速度运动,另一动点Q从A出发沿着AC边以4cm/s的速度运动,P、Q两点同时出发,运动时间为t(s).
(1)若△PCQ的面积是△ABC面积的![]() ,求t的值?
,求t的值?
(2)△PCQ的面积能否与四边形ABPQ面积相等?若能,求出t的值;若不能,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,
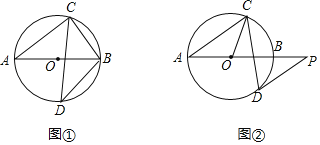
(1)如图①,若D为弧AB的中点,求∠ABC和∠ABD的大小;
(2)如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面直角坐标系中,设一次函数y1=mx+n(m,n为常数,且m≠0,m≠-n)与反比例函数y2=![]() .
.
(1)若y1与y2的图象有交点(1,5),且n=4m,当y1≥5时,y2的取值范围;
(2)若y1与y2的图象有且只有一个交点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
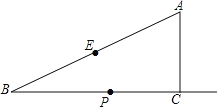
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润.下列结论错误的是( )
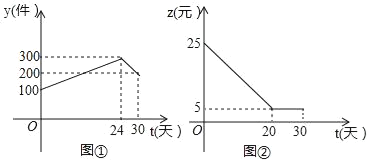
A.第24天的销售量为300件
B.第10天销售一件产品的利润是15元
C.第27天的日销售利润是1250元
D.第15天与第30天的日销售量相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线经过
,抛物线经过![]() 、
、![]() 、
、![]() 三点,连接
三点,连接![]() 、
、![]() 、
、![]() ,线段
,线段![]() 交
交![]() 轴于点
轴于点![]() ,已知实数
,已知实数![]() 、
、![]()
![]() 分别是方程
分别是方程![]() 的两根.
的两根.
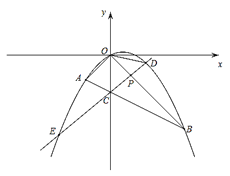
(1)求抛物线的解析式;
(2)若点![]() 为线段
为线段![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合),直线
重合),直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点(点
两点(点![]() 在
在![]() 轴右侧),连接
轴右侧),连接![]() 、
、![]() .
.
①求![]() 面积的最大值,并写出此时点
面积的最大值,并写出此时点![]() 的坐标;②当
的坐标;②当![]() 为等腰三角形时,请直接写出点
为等腰三角形时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com