
【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,
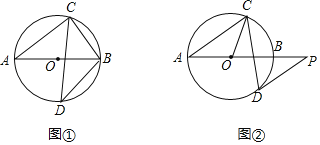
(1)如图①,若D为弧AB的中点,求∠ABC和∠ABD的大小;
(2)如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
【答案】(1)∠ABC=52°∠ABD=45°;(2)∠OCD=26°.
【解析】
(1)根据圆周角和圆心角的关系和图形可求∠ABC和∠ABD的大小.
(2)根据题意和平行线的性质,切线的性质可以求得∠OCD的度数.
(1)∵AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,
∴∠ACB=90°,
∴∠ABC=∠ACB-∠BAC=90°-38°=52°,
∵D为弧AB的中点,∠AOB=180°,
∴∠AOD=90°,
∴∠ABD=45°;
(2)连接OD,

∵DP切⊙O于点D,
∴OD⊥DP,即∠ODP=90°,
由DP∥AC,又∠BAC=38°,
∴∠P=∠BAC=38°,
∵∠AOD是△ODP的一个外角,
∴∠AOD=∠P+∠ODP=128°,
∴∠ACD=64°,
∵OC=OA,∠BAC=38°,
∴∠OCA=∠BAC=38°,
∴∠OCD=∠ACD-∠OCA=64°-38°=26°.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(0,1)、B(3,3)、C(1,3).
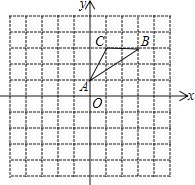
(1) 画出△ABC关于点O的中心对称图形△A1B1C1
(2) 画出△ABC绕原点O逆时针旋转90°的△A2B2C2,直接写出点C2的坐标为______.
(3) 若△ABC内一点P(m,n)绕原点O逆时针旋转90°的对应点为Q,则Q的坐标为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕着点C顺时针旋转50°后得到△A′B′C′.若∠A=40°,∠B′=110°,则∠BCA′的度数是( )

A.90°B.80°C.50°D.30°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人分别站在相距 6 米的 A , B 两点练习打羽毛球,已知羽毛球飞行的路线为抛物线的一部分,甲在离地面 1 米的C 处发出一球,乙在离地面 1.5 米的 D 处成功击球,球飞行过程中的最高点 H 与甲的水平距离 AE 为 4 米,现以 A 为原点,直线 AB 为 x 轴, 建立平面直角坐标系(如图所示).
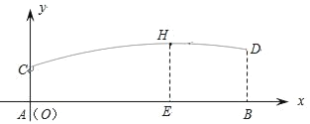
(1)求羽毛球飞行的路线所在的抛物线的表达式;
(2)求羽毛球飞行的最高高度。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 中,
中,![]() ,点
,点![]() 是
是![]() 内一点,连接
内一点,连接![]() ,且
,且![]() ,设
,设![]() .
.
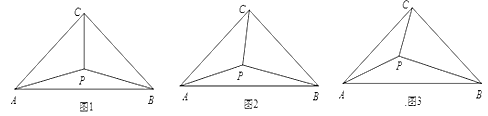
(1)如图1,若![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 至
至![]() ,连结
,连结![]() ,易证
,易证![]() 为等边三角形,则
为等边三角形,则![]() ,
,![]() ;
;
(2)如图2,若![]() ,则
,则![]() ,
,![]() ;
;
(3)如图3,试猜想![]() 和
和![]() 之间的数量关系,并给予证明.
之间的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与一次函数
与一次函数![]() ,令W=
,令W=![]() .
.
(1)若![]() 、
、![]() 的函数图像交于x轴上的同一点.
的函数图像交于x轴上的同一点.
①求![]() 的值;
的值;
②当![]() 为何值时,W的值最小,试求出该最小值;
为何值时,W的值最小,试求出该最小值;
(2)当![]() 时,W随x的增大而减小.
时,W随x的增大而减小.
①求![]() 的取值范围;
的取值范围;
②求证: ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】形如![]() 的函数称为反比例函数,我们定义,如果一次函数
的函数称为反比例函数,我们定义,如果一次函数![]() 和反比例函数
和反比例函数![]() 的系数a、b、c(abc≠0)满足
的系数a、b、c(abc≠0)满足![]() ,则称二次函数
,则称二次函数![]() 为一次函数函数y1和反比例函数y2的“调和二次函数”.
为一次函数函数y1和反比例函数y2的“调和二次函数”.
(1)试判断一次函数![]() 反比例函数
反比例函数![]() 的“调和二次函数”是否存在,并说明理;
的“调和二次函数”是否存在,并说明理;
(2)若二次函数 y3 m 1 x2 2mx 4 是某一次函数和反比例函数的“调和二次函数”,试求该一次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com