
ЁОЬтФПЁПаЮШч![]() ЕФКЏЪ§ГЦЮЊЗДБШР§КЏЪ§ЃЌЮвУЧЖЈвхЃЌШчЙћвЛДЮКЏЪ§
ЕФКЏЪ§ГЦЮЊЗДБШР§КЏЪ§ЃЌЮвУЧЖЈвхЃЌШчЙћвЛДЮКЏЪ§![]() КЭЗДБШР§КЏЪ§
КЭЗДБШР§КЏЪ§![]() ЕФЯЕЪ§aЁЂbЁЂc(abcЁй0ЃЉТњзу
ЕФЯЕЪ§aЁЂbЁЂc(abcЁй0ЃЉТњзу![]() ЃЌдђГЦЖўДЮКЏЪ§
ЃЌдђГЦЖўДЮКЏЪ§![]() ЮЊвЛДЮКЏЪ§КЏЪ§y1КЭЗДБШР§КЏЪ§y2ЕФЁАЕїКЭЖўДЮКЏЪ§ЁБ.
ЮЊвЛДЮКЏЪ§КЏЪ§y1КЭЗДБШР§КЏЪ§y2ЕФЁАЕїКЭЖўДЮКЏЪ§ЁБ.
(1)ЪдХаЖЯвЛДЮКЏЪ§![]() ЗДБШР§КЏЪ§
ЗДБШР§КЏЪ§![]() ЕФЁАЕїКЭЖўДЮКЏЪ§ЁБЪЧЗёДцдкЃЌВЂЫЕУїРэЃЛ
ЕФЁАЕїКЭЖўДЮКЏЪ§ЁБЪЧЗёДцдкЃЌВЂЫЕУїРэЃЛ
(2)ШєЖўДЮКЏЪ§ y3 m 1 x2 2mx 4 ЪЧФГвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФЁАЕїКЭЖўДЮКЏЪ§ЁБЃЌЪдЧѓИУвЛДЮКЏЪ§ЕФНтЮіЪН.
ЁОД№АИЁПЃЈ1ЃЉДцдкЃЌРэгЩМћНтЮіЃЛЃЈ2ЃЉвЛДЮКЏЪ§ЕФНтЮіЪНЮЊy=ЃЈ1+![]() ЃЉx+4+2
ЃЉx+4+2![]() Лђy=ЃЈ1-
Лђy=ЃЈ1-![]() ЃЉx+4-2
ЃЉx+4-2![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЁАЕїКЭЖўДЮКЏЪ§ЁБЕФЖЈвхМДПЩЧѓНтЃЛ
ЃЈ2ЃЉИљОнЁАЕїКЭЖўДЮКЏЪ§ЁБЕУЕНЙигкmЕФЗНГЬЃЌНтГіМДПЩЧѓНт.
ЃЈ1ЃЉЁпвЛДЮКЏЪ§![]() ЗДБШР§КЏЪ§
ЗДБШР§КЏЪ§![]()
a=2,b=6,c=3,
Ёр![]() ЃЌ
ЃЌ![]()
Ёр![]()
ЙЪЁАЕїКЭЖўДЮКЏЪ§ЁБДцдкЃЛ
ЃЈ2ЃЉЁпЖўДЮКЏЪ§ y3 m 1 x2 2mx 4 ЪЧФГвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФЁАЕїКЭЖўДЮКЏЪ§ЁБЃЌ
a=m-1,b=2m,c=4,
Ёп![]()
Ёр![]() ЃЌШЅЗжФИЕУm2-4m+1=0
ЃЌШЅЗжФИЕУm2-4m+1=0
ЧѓЕУm1=2+![]() ЃЌm2=2-
ЃЌm2=2-![]()
ЙЪИУвЛДЮКЏЪ§ЕФНтЮіЪНЮЊy=ЃЈ1+![]() ЃЉx+4+2
ЃЉx+4+2![]() Лђy=ЃЈ1-
Лђy=ЃЈ1-![]() ЃЉx+4-2
ЃЉx+4-2![]() .
.


 ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ
ПкЫуЬтПЈМггІгУЬтМЏбЕЯЕСаД№АИ злКЯздВтЯЕСаД№АИ
злКЯздВтЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁЙКНјвЛХњ 30 ЭпЕФ LED ЕЦХнКЭЦеЭЈАзГуЕЦХнНјааЯњЪлЃЌЦфНјМлгыБъМлШчЯТБэЃК
LED ЕЦХн | ЦеЭЈАзГуЕЦХн | |
НјМлЃЈдЊЃЉ | 45 | 25 |
БъМлЃЈдЊЃЉ | 60 | 30 |

ЃЈ1ЃЉИУЩЬГЁЙКНјСЫ LED ЕЦХнгыЦеЭЈАзГуЕЦХнЙВ 300 ИіЃЌLED ЕЦХнАДБъМлНјааЯњЪлЃЌЖјЦеЭЈ АзГуЕЦХнДђОХелЯњЪлЃЌЕБЯњЪлЭъетХњЕЦХнКѓПЩЛёРћ 3 200 дЊЃЌЧѓИУЩЬГЁЙКНј LED ЕЦХнгы ЦеЭЈАзГуЕЦХнЕФЪ§СПЗжБ№ЮЊЖрЩйИіЃП
ЃЈ2ЃЉгЩгкДКНкЦкМфШШЯњЃЌКмПьНЋСНжжЕЦХнЯњЪлЭъЃЌШєИУЩЬГЁМЦЛЎдйДЮЙКНјетСНжжЕЦХн 120 ИіЃЌ дкВЛДђелЕФЧщПіЯТЃЌЧыЮЪШчКЮНјЛѕЃЌЯњЪлЭъетХњЕЦХнЪБЛёРћзюЖрЧвВЛГЌЙ§НјЛѕМлЕФ 30%ЃЌ ВЂЧѓГіДЫЪБетХњЕЦХнЕФзмРћШѓЮЊЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊABЪЧЁбOЕФжБОЖЃЌЯвCDгыABЯрНЛЃЌЁЯBAC=38ЁуЃЌ
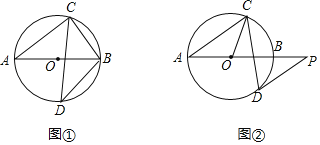
ЃЈ1ЃЉШчЭМЂйЃЌШєDЮЊЛЁABЕФжаЕуЃЌЧѓЁЯABCКЭЁЯABDЕФДѓаЁЃЛ
ЃЈ2ЃЉШчЭМЂкЃЌЙ§ЕуDзїЁбOЕФЧаЯпЃЌгыABЕФбгГЄЯпНЛгкЕуPЃЌШєDPЁЮACЃЌЧѓЁЯOCDЕФДѓаЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
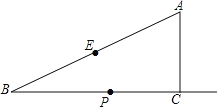
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯACBЃН90ЁуЃЌЁЯBЃН30ЁуЃЌACЃН2ЃЌEЮЊаББпABЕФжаЕуЃЌЕуPЪЧЩфЯпBCЩЯЕФвЛИіЖЏЕуЃЌСЌНгAPЁЂPEЃЌНЋЁїAEPбизХБпPEелЕўЃЌелЕўКѓЕУЕНЁїEPAЁфЃЌЕБелЕўКѓЁїEPAЁфгыЁїBEPЕФжиЕўВПЗжЕФУцЛ§ЧЁКУЮЊЁїABPУцЛ§ЕФЫФЗжжЎвЛЃЌдђДЫЪБBPЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
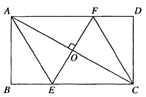
ЁОЬтФПЁПШчЭМЃЌдкЫФБпаЮABCDжаЃЌADЁЮBCЃЌЁЯABC=ЁЯADC=90ЁуЃЌЖдНЧЯпACЃЌBDНЛгкЕуOЃЌDEЦНЗжЁЯADCНЛBCгкЕуEЃЌСЌНгOEЃЎ
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮABCDЪЧОиаЮЃЛ
ЃЈ2ЃЉШєAB=2ЃЌЧѓЁїOECЕФУцЛ§ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЪЧБОЕиЧјвЛжжВњЦЗ30ЬьЕФЯњЪлЭМЯѓЃЌЭМЂйЪЧВњЦЗШеЯњЪлСПyЃЈЕЅЮЛЃКМўЃЉгыЪБМфtЃЈЕЅЮЛЃКЬьЃЉЕФКЏЪ§ЙиЯЕЃЌЭМЂкЪЧвЛМўВњЦЗЕФЯњЪлРћШѓzЃЈЕЅЮЛЃКдЊЃЉгыЪБМфtЃЈЕЅЮЛЃКЬьЃЉЕФКЏЪ§ЙиЯЕЃЌвбжЊШеЯњЪлРћШѓЃНШеЯњЪлСПЁСвЛМўВњЦЗЕФЯњЪлРћШѓЃЎЯТСаНсТлДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ
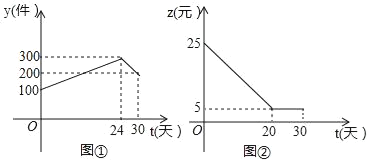
A.Ек24ЬьЕФЯњЪлСПЮЊ300Мў
B.Ек10ЬьЯњЪлвЛМўВњЦЗЕФРћШѓЪЧ15дЊ
C.Ек27ЬьЕФШеЯњЪлРћШѓЪЧ1250дЊ
D.Ек15ЬьгыЕк30ЬьЕФШеЯњЪлСПЯрЕШ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
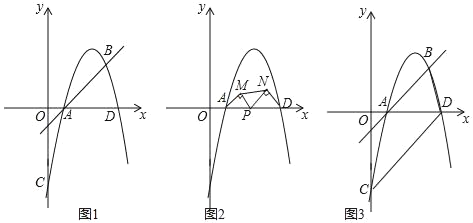
ЁОЬтФПЁПШчЭМ1ЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌжБЯпyЃНxЉ1гыХзЮяЯпyЃНЉx2+bx+cНЛгкAЁЂBСНЕуЃЌЦфжаAЃЈmЃЌ0ЃЉЁЂBЃЈ4ЃЌnЃЉЃЌИУХзЮяЯпгыyжсНЛгкЕуCЃЌгыxжсНЛгкСэвЛЕуDЃЎ
ЃЈ1ЃЉЧѓmЁЂnЕФжЕМАИУХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌШєЕуPЮЊЯпЖЮADЩЯЕФвЛЖЏЕуЃЈВЛгыAЁЂDжиКЯЃЉЃЌЗжБ№вдAPЁЂDPЮЊаББпЃЌдкжБЯпADЕФЭЌВрзїЕШбќжБНЧЁїAPMКЭЕШбќжБНЧЁїDPNЃЌСЌНгMNЃЌЪдШЗЖЈЁїMPNУцЛ§зюДѓЪБPЕуЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌСЌНгBDЁЂCDЃЌдкЯпЖЮCDЩЯЪЧЗёДцдкЕуQЃЌЪЙЕУвдAЁЂDЁЂQЮЊЖЅЕуЕФШ§НЧаЮгыЁїABDЯрЫЦЃЌШєДцдкЃЌЧыжБНгаДГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКЖўДЮКЏЪ§![]()
ЃЈ1ЃЉЭЈЙ§ХфЗННЋЫќаДГЩ![]() ЕФаЮЪН.
ЕФаЮЪН.
ЃЈ2ЃЉЕБ![]() ЪБЃЌКЏЪ§газю жЕЃЌЪЧ .
ЪБЃЌКЏЪ§газю жЕЃЌЪЧ .
ЃЈ3ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјдіДѓЃЛЃЉЕБ
ЕФдіДѓЖјдіДѓЃЛЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјМѕаЁ.
ЕФдіДѓЖјМѕаЁ.
ЃЈ4ЃЉИУКЏЪ§ЭМЯѓгЩ![]() ЕФЭМЯѓОЙ§дѕбљЕФЦНвЦЕУЕНЃП
ЕФЭМЯѓОЙ§дѕбљЕФЦНвЦЕУЕНЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЙ§ОиаЮ![]() ЕФЖдНЧЯп
ЕФЖдНЧЯп![]() ЕФжаЕу
ЕФжаЕу![]() зї
зї![]() ЃЌНЛ
ЃЌНЛ![]() БпгкЕу
БпгкЕу![]() ЃЌНЛ
ЃЌНЛ![]() БпгкЕу
БпгкЕу![]() ЃЌЗжБ№СЌНг
ЃЌЗжБ№СЌНг![]() ЁЂ
ЁЂ![]() ЃЎШє
ЃЎШє![]() ЃЌ
ЃЌ![]() ЃЌдђ
ЃЌдђ![]() ЕФГЄЮЊЃЈ ЃЉ
ЕФГЄЮЊЃЈ ЃЉ
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com