
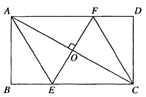
【题目】如图,过矩形![]() 的对角线
的对角线![]() 的中点
的中点![]() 作
作![]() ,交
,交![]() 边于点
边于点![]() ,交
,交![]() 边于点
边于点![]() ,分别连接
,分别连接![]() 、
、![]() .若
.若![]() ,
,![]() ,则
,则![]() 的长为( )
的长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
求出∠ACB=∠DAC,然后利用“角角边”证明△AOF和△COE全等,根据全等三角形对应边相等可得OE=OF,再根据对角线互相垂直平分的四边形是菱形得到四边形AECF是菱形,再求出∠ECF=60°,然后判断出△CEF是等边三角形,根据等边三角形的三条边都相等可得EF=CF,根据矩形的对边相等可得CD=AB,然后求出CF,从而得解.
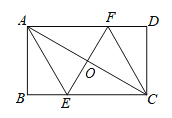
解:如图:∵矩形对边AD//BC,
∴∠ACB=∠DAC,
∵O是AC的中点,
∴AO=CO,
在△AOF和△COE中,
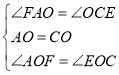
∴△AOF≌ACOE(ASA),
∴OE=OF,
又∵EF⊥AC,
∴四边形AECF是菱形,
∵∠DCF=30°,
∴.∠ECF=90°-30°=60°,
∴△CEF是等边三角形,
∴EF=CF,
∵AB=![]() ,
,
∴CD=AB=![]() ,
,
∵∠DCF=30°,
∴![]()
∴EF=2,故选A.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】形如![]() 的函数称为反比例函数,我们定义,如果一次函数
的函数称为反比例函数,我们定义,如果一次函数![]() 和反比例函数
和反比例函数![]() 的系数a、b、c(abc≠0)满足
的系数a、b、c(abc≠0)满足![]() ,则称二次函数
,则称二次函数![]() 为一次函数函数y1和反比例函数y2的“调和二次函数”.
为一次函数函数y1和反比例函数y2的“调和二次函数”.
(1)试判断一次函数![]() 反比例函数
反比例函数![]() 的“调和二次函数”是否存在,并说明理;
的“调和二次函数”是否存在,并说明理;
(2)若二次函数 y3 m 1 x2 2mx 4 是某一次函数和反比例函数的“调和二次函数”,试求该一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自从湖南与欧洲的“湘欧快线”开通后,我省与欧洲各国经贸往来日益频繁,某欧洲客商准备在湖南采购一批特色商品,经调查,用16 000元采购A型商品的件数是用7 500元采购B型商品的件数的2倍,一件A型商品的进价比一件B型商品的进价多10元.
(1)求一件A,B型商品的进价分别为多少元?
(2)若该欧洲客商购进A,B型商品共250件进行试销,其中A型商品的件数不大于B型的件数,且不小于80件,已知A型商品的售价为240元/件,B型商品的售价为220元/件,且全部售出.设购进A型商品m件,求该客商销售这批商品的利润v与m之间的函数解析式,并写出m的取值范围;
(3)在(2)的条件下,欧洲客商决定在试销活动中每售出一件A型商品,就从一件A型商品的利润中捐献慈善资金a元,求该客商售完所有商品并捐献慈善资金后获得的最大收益.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明根据学习函数的经验,对函数y=x+![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小明的探究过程,请补充完整:
(1)函数y=x+![]() 的自变量x的取值范围是_____.
的自变量x的取值范围是_____.
(2)下表列出了y与x的几组对应值,请写出m,n的值:m=_____,n=_____;
x | … | ﹣3 | ﹣2 | ﹣1 | ﹣ | ﹣ |
|
| 1 | 2 | 3 | 4 | … |
y | … | ﹣ | ﹣ | ﹣2 | ﹣ | ﹣ | m |
| 2 |
| n |
| … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)结合函数的图象,请完成:
①当y=﹣![]() 时,x=_____.
时,x=_____.
②写出该函数的一条性质_____.
③若方程x+![]() =t有两个不相等的实数根,则t的取值范围是_____.
=t有两个不相等的实数根,则t的取值范围是_____.
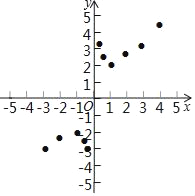
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应市委市政府提出的建设“绿色襄阳”的号召,我市某单位准备将院内一块长30m,宽20m的长方形空地,建成一个矩形花园.要求在花园中修两条纵向平行和一条横向弯折的小道,剩余的地方种植花草,如图所示,要使种植花草的面积为532m2,那么小道进出口的宽度应为多少米?(注:所有小道进出口的宽度相等,且每段小道均为平行四边形)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的y与x的部分对应值如表:则下列判断中正确的是( )
x | … | ﹣1 | 0 | 1 | 3 | … |
y | … | ﹣3 | 1 | 3 | 1 | … |
A. 抛物线开口向上B. 抛物线与y轴交于负半轴
C. 当x=4时,y>0D. 方程ax2+bx+c=0的正根在3与4之间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B的坐标分别为(4,0),(3,2).
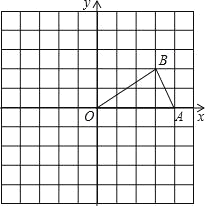
(1)画出△AOB关于原点O对称的图形△COD;
(2)将△AOB绕点O按逆时针方向旋转90°得到△EOF,画出△EOF;
(3)点D的坐标是 ,点F的坐标是 ,此图中线段BF和DF的关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com