
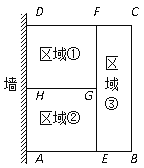
【题目】为了节省材料,某养殖户利用墙 (墙足够长)为一边,用总长为80m的篱笆围成了如图所示的①②③三块矩形区域养鸡场,而且这三块矩形区域的面积相等.若矩形区域ABCD的面积为300m2.求BC的长。
【答案】BC的长为20m.
【解析】
设BC的长为xm,根据三个矩形的面积相等,得到矩形AEFD面积是矩形BCFE面积的2倍,可以得出AE=2BE,设BE=a,则AE=2a,根据“篱笆总长为80m”得出a与x的一个等式,把a用x表示出来,再根据“矩形区域ABCD的面积为300m2”列出一个含x的方程,解此方程即可得出答案.
解:设BC的长为xm
∵三块矩形区域的面积相等,∴矩形AEFD面积是矩形BCFE面积的2倍,
∴AE=2BE,设BE=a,则AE=2a,
∴8a+2x=80,∴a=-![]() x+10,AB=3a=-
x+10,AB=3a=-![]() x+30,
x+30,
∴(-![]() x+30)x=300 解得:x1=x2=20
x+30)x=300 解得:x1=x2=20
答:BC的长为20m.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】今年,我国政府为减轻农民负担,决定在5年内免去农业税.某乡今年人均上缴农业税25元,若两年后人均上缴农业税为16元,假设这两年降低的百分率相同.
(1)求降低的百分率;
(2)若小红家有4人,明年小红家减少多少农业税?
查看答案和解析>>
科目:初中数学 来源: 题型:
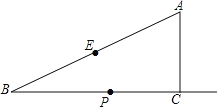
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AC=2,E为斜边AB的中点,点P是射线BC上的一个动点,连接AP、PE,将△AEP沿着边PE折叠,折叠后得到△EPA′,当折叠后△EPA′与△BEP的重叠部分的面积恰好为△ABP面积的四分之一,则此时BP的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位:天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润.下列结论错误的是( )
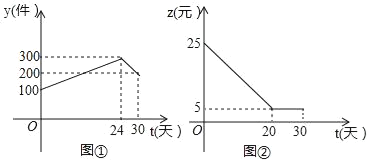
A.第24天的销售量为300件
B.第10天销售一件产品的利润是15元
C.第27天的日销售利润是1250元
D.第15天与第30天的日销售量相等
查看答案和解析>>
科目:初中数学 来源: 题型:
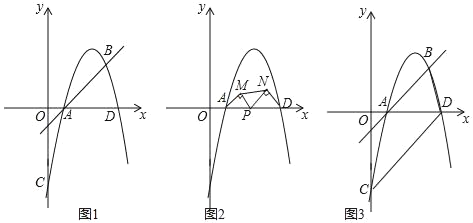
【题目】如图1,在平面直角坐标系中,直线y=x﹣1与抛物线y=﹣x2+bx+c交于A、B两点,其中A(m,0)、B(4,n),该抛物线与y轴交于点C,与x轴交于另一点D.
(1)求m、n的值及该抛物线的解析式;
(2)如图2,若点P为线段AD上的一动点(不与A、D重合),分别以AP、DP为斜边,在直线AD的同侧作等腰直角△APM和等腰直角△DPN,连接MN,试确定△MPN面积最大时P点的坐标;
(3)如图3,连接BD、CD,在线段CD上是否存在点Q,使得以A、D、Q为顶点的三角形与△ABD相似,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,用一段25m的篱笆圈成一个一边靠墙的矩形菜园,墙长12m,为方便进出,在垂直于墙的一边留一个1m宽的门.
(1)当菜园面积为80m2时,所用矩形菜园的长、宽分别为多少?
(2)所围成的矩形菜园的面积能为90m2吗?如果能,请求此时菜园的长和宽;如果不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:二次函数![]()
(1)通过配方将它写成![]() 的形式.
的形式.
(2)当![]() 时,函数有最 值,是 .
时,函数有最 值,是 .
(3)当![]() 时,
时,![]() 随
随![]() 的增大而增大;)当
的增大而增大;)当![]() 时,
时,![]() 随
随![]() 的增大而减小.
的增大而减小.
(4)该函数图象由![]() 的图象经过怎样的平移得到?
的图象经过怎样的平移得到?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,抛物线经过
,抛物线经过![]() 、
、![]() 、
、![]() 三点,连接
三点,连接![]() 、
、![]() 、
、![]() ,线段
,线段![]() 交
交![]() 轴于点
轴于点![]() ,已知实数
,已知实数![]() 、
、![]()
![]() 分别是方程
分别是方程![]() 的两根.
的两根.
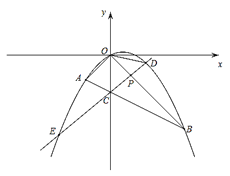
(1)求抛物线的解析式;
(2)若点![]() 为线段
为线段![]() 上的一个动点(不与点
上的一个动点(不与点![]() 、
、![]() 重合),直线
重合),直线![]() 与抛物线交于
与抛物线交于![]() 、
、![]() 两点(点
两点(点![]() 在
在![]() 轴右侧),连接
轴右侧),连接![]() 、
、![]() .
.
①求![]() 面积的最大值,并写出此时点
面积的最大值,并写出此时点![]() 的坐标;②当
的坐标;②当![]() 为等腰三角形时,请直接写出点
为等腰三角形时,请直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交舡于点G,连接DG.
(1)求证:四边形EFDG是菱形;
(2) 求证: ![]() ;
;
(3)若AG=6,EG=2![]() ,求BE的长.
,求BE的长.
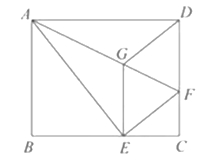
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com