练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    12．已知：$\frac{2x-3}{x+1}=2+\frac{m}{x+1}$，则m=-5．

    分析 已知等式右边通分并利用同分母分式的减法法则计算，即可确定出m的值．

    解答 解：$\frac{2x-3}{x+1}$=2+$\frac{m}{x+1}$=$\frac{2x+2+m}{x+1}$，
    可得2x-3=2x+2+m，
    解得：m=-5，
    故答案为：-5

    点评 此题考查了分式的加减法，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    2．解方程．
    （1）（x+1）（x-1）+2（x+3）=8
    （2）2（x-3）=3x（x-3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

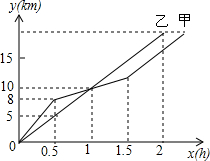    3．在全民健身环城越野赛中，甲、乙两名选手各自的行程y（km）随时间t（h）变化的图象（全程）如图所示．有下列说法：①起跑后2h内，甲在乙的前面；②第1h时两人都跑了l0km；③甲比乙先到达终点；④两人都跑了20km．其中正确的说法有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

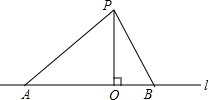    20．作图并回答：过点P作直线l的垂线PO，垂足为O，连接PA、PB；比较线段PO、PA、PB的长短，并按小到大的顺序排列为PO＜PB＜PA．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．课文片段学习：
    下面这个方程含有三个未知数，每个方程中含未知数的项的次数都是1，并且一共有三个方程，像这样的方程组叫做三元一次方程组．
    $\left\{\begin{array}{l}{x+y+z=12①}\\{x+2y+5z=22②}\\{x=4y③}\end{array}\right.$
    怎样解三元一次方程组呢？我们知道，二元一次方程组可以利用代入法或加减法消去一个未知数，化成一元一次方程求解．那么，能不能用同样的思路，用代入法或加减法消去三元一次方程组的一个未知数，把它化成二元一次方程组呢？
    依照前面学过的代入法，我们可以把③分别代入①、②，得到两个只含y，z方程：
    4y+y+z=12
    4y+2y+5z=22
    把它们组成方程组$\left\{\begin{array}{l}5y+z=12\\ 6y+5z=22\end{array}\right.$
    得到二元一次方程组之后，就不难求出y和z，进而可求出x．
    从上面的分析可以看出，解三元一次方程组的基本思路是：通过“代入”或“加减”进行消元，把“三元”化为“二元”，使解三元一次方程组转化为解二元一次方程组，进而再转化为解一元一次方程．这与解二元一次方程组的思路是一样的．

    根据以上学习，解以下三元一次方程组：
    （1）$\left\{\begin{array}{l}{y=2x-7}\\{5x+3y+2z=2}\\{3x-4z=4}\end{array}\right.$                 （2）$\left\{\begin{array}{l}2x+4y+3z=9\\ 3x-2y+5z=11\\ 5x-6y+7z=13\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

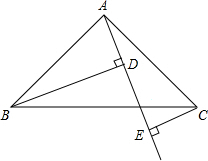    17．如图，Rt△ABC中，AB=AC，∠BAC=90°，直线AE是经过点A的任一直线，BD⊥AE于D，CE⊥AE于E，若BD＞CE，试解答：
    （1）AD与CE的大小关系如何？请说明理由．
    （2）若BD=5，CE=2，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．在上完数学课后，王磊发现操场上的旗杆与旁边一棵大树的影子好像平行，但他不敢肯定，此时他最好的办法是（　　）
    A．找来三角板、直尺，通过平移三角板来验证影子是否平行
    B．相信自己，两个影子就是平行的
    C．构造几何模型，用已学过的知识证明
    D．作一直线截两影子，并用量角器测出同位角的度数，若相等则影子平行

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．随州特产--蜜枣，零售价为6元/袋，A商店的优惠方案是：第一袋按原价，其余七五折优惠；B商店的优惠方案是：全部按原价的八折优惠
    （1）李明想买一袋蜜枣，从节约的角度出发，他应到哪家商店购买？为什么？
    （2）刘涛想买10袋蜜枣，从节约的角度出发，他应到哪家商店购买？
    （3）当买几袋蜜枣时，到两个商店所用的钱数都一样？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．如图，B，C分别在△ADE的边AD，AE上，且AC=6，AB=5，EC=4，DB=7，则BC：DE=$\frac{1}{2}$．

    查看答案和解析>>

    同步练习册答案