
����Ŀ���Ķ�������ϣ�
![]()
![]()
![]()
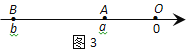
��A��B�������Ϸֱ��ʾʵ��a��b��A��B����֮��ľ����ʾΪ�OAB�O.��A��B��������һ����ԭ��ʱ���������A��ԭ�㣬��ͼ1���OAB�O���OOB�O���Ob�O���Oa-b�O����A��B���㶼����ԭ��ʱ����ͼ2����A��B����ԭ����ұߨOAB�O=�OOB�O-�OOA�O=�Ob�O-�Oa�O=![]() =�Oa-b�O����ͼ3������A��B����ԭ�����ߣ��OAB�O���OOB�O-�OOA�O���Ob�O-�Oa�O=
=�Oa-b�O����ͼ3������A��B����ԭ�����ߣ��OAB�O���OOB�O-�OOA�O���Ob�O-�Oa�O=![]() =�Oa-b�O����ͼ4������A��B��ԭ������ߣ��OAB�O���OOB�O+�OOA�O���Oa�O+�Ob�O=
=�Oa-b�O����ͼ4������A��B��ԭ������ߣ��OAB�O���OOB�O+�OOA�O���Oa�O+�Ob�O=![]() =�Oa-b�O.
=�Oa-b�O.
�ش��������⣺
��1�������ϱ�ʾ2��5������֮��ľ�����_____�������ϱ�ʾ1�ͣ�3������֮��ľ�����______.
��2������������A��ʾ������x����B��ʾ�����ǣ�2�����A��B֮��ľ�����_____�����OAB�O��2����ôxΪ______.
��3����x��_____ʱ������ʽ![]() .
.
��4������A��ʾ������-1����B���A�ľ�����10���ҵ�B�ڵ�A���Ҳ࣬����P��Qͬʱ��A��B�����������������˶�����P���ٶ���ÿ��3����λ���ȣ���Q���ٶ���ÿ��![]() ����λ���ȣ����˶������P���Q֮��ľ���Ϊ5����λ���� ������д����Ҫ�������̣�
����λ���ȣ����˶������P���Q֮��ľ���Ϊ5����λ���� ������д����Ҫ�������̣�
���𰸡���1��3��4����2��![]() ��0��-4����3��-3��2����4���˶�2���6��ʱ����P���Q֮��ľ���Ϊ5����λ����.
��0��-4����3��-3��2����4���˶�2���6��ʱ����P���Q֮��ľ���Ϊ5����λ����.
��������
��1������������A��B����֮��ľ���|AB|=|a-b|��������ֵ���þ���ֵ���������������ľ��룻��2������������A��B����֮��ľ���|AB|=|a-b|���ɵô𰸣���3���ֱ�����x<-2��-2��x<1��x��1ʱ�����ݾ���ֵ������ȥ������ֵ�������x��һԪһ�η��̼������x��ֵ����4���ֵ�P�ϵ�Qǰ�͵�P�ϵ�Q���������5����λ����������������ݾ���=�ٶ���ʱ�䣬�ֱ����ʱ�伴��.
��1����������A��B����֮��ľ���|AB|=|a-b|��
���ʾ2��5������֮��ľ�����![]() =3����ʾ1��-3������֮��ľ�����
=3����ʾ1��-3������֮��ľ�����![]() =4.
=4.
�ʴ�Ϊ��3��4
��2����������A��B����֮��ľ���|AB|=|a-b|��
��������x�ͣ�2֮��ľ�����![]() =
=![]() ��
��
�ߨOAB�O��2��
��![]() =2��
=2��
x+2=2��x+2=-2��
��ã�x=0��x=-4��
�ʴ�Ϊ��![]() ��0��-4
��0��-4
��3��![]() ��
��
�ٵ�x<-2ʱ��-(x+2)-(x-1)=5��
��ã�x=-3
�ڵ�-2��x<1ʱ��x+2-(x-1)=5��
1=5��������ʵ�ʣ�x�����ڣ�
�۵�x��1ʱ��x+2+x-1=5��
��ã�x=2��
����������x=-3��x=2ʱ��![]() ��
��
�ʴ�Ϊ��-3��2
��4�����˶�t���P���Q֮��ľ���Ϊ5����λ���ȣ�
�ٵ���P�ϵ�Qǰ�������5����λ����ʱ��
10+![]() t-3t=5��
t-3t=5��
��ã�t=2��
�ڵ���P�ϵ�Q���������5����λ����ʱ��
3t-(10+![]() t)=5��
t)=5��
��ã�t=6.
���˶�2���6��ʱ����P���Q֮��ľ���Ϊ5����λ����.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������,��P��ʾ������a,��P1��ʾ������![]() ,���dz�����P1�ǵ�P����ص���,��֪������A1����ص�ΪA2,��A2����ص�ΪA3,��A3����ص�ΪA4,�������εõ���A1��A2��A3,A4,��,An����A1�������ʾ������
,���dz�����P1�ǵ�P����ص���,��֪������A1����ص�ΪA2,��A2����ص�ΪA3,��A3����ص�ΪA4,�������εõ���A1��A2��A3,A4,��,An����A1�������ʾ������![]() ,���A2109�������ϱ�ʾ������__________.
,���A2109�������ϱ�ʾ������__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬BD�ǽ�ƽ���ߣ���O��AB�ϣ��Ե�OΪԲ�ģ�OBΪ�뾶��Բ������D����BC�ڵ�E��
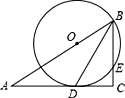
��1����֤��AC�ǡ�O�����ߣ�
��2����OB=5��CD=4����BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ��ά��������Ȩ�ͺ���Ȩ�������ಿ�Ŷ��ҹ��캣ʵ���˳�̬��Ѳ����������ͼ������ִ��Ѳ������ĺ��ബ��ÿСʱ50������ٶ������������У���![]() ����õ���
����õ���![]() �ڱ�ƫ��
�ڱ�ƫ��![]() �����ϣ���������1Сʱ����
�����ϣ���������1Сʱ����![]() ������ʱ��õ���
������ʱ��õ���![]() �ڱ�ƫ��
�ڱ�ƫ��![]() �����ϣ�
�����ϣ�
��1����![]() �Ķ�����
�Ķ�����
��2����֪�ڵ���![]() ����Χ25�������а������ʺ��ബ�����������������Ƿ�ȫ��
����Χ25�������а������ʺ��ബ�����������������Ƿ�ȫ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڽ�����AB�ϣ�����35 m������������AE������һ������CD�Ķ���D������������A��������Ϊ45������������E��������Ϊ37�㣮�����������ľ���BC��
(�����:sin37����0.6��cos37����0.8�� tan37����0.75)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����������ʽ��3+2=3��2-1��4+![]() ��4��
��4��![]() -1�������������£�
-1�������������£�
���dz�ʹ��ʽa+b=ab-1������һ��������a��bΪ�������������ԡ�����Ϊ��a��b�����磺���ԣ�3��2������4��![]() �����ǡ������������ԡ���
�����ǡ������������ԡ���
��1�����ԣ�-2��1������5��![]() �����ǡ������������ԡ����� ��
�����ǡ������������ԡ����� ��
��2������a��3���ǡ������������ԡ�����a��ֵ��
��3������m��n���ǡ������������ԡ�����-n��-m�� �������������ԡ�����ǡ��������ǡ���ȷ��������
��4������д��һ�Է��������ġ������������ԡ� ��ע�⣺��������Ŀ�����еġ������������ԡ��ظ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ�����������ĸ����ۣ���4ac��b2��0����4a+c��2b����3b+2c��0����m��am+b��+b��a��m�٩�1����������ȷ���۵���_________��ֻ����ţ�.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
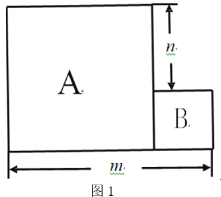
����Ŀ����1����ͼ1����֪A��B�����߳�����ȵ�������ֽƬ���ŷ��ã���m7��n3������A��B����������ֽƬ�����֮�ͣ�
��2����ͼ1����m��n��ʾA��B����������ֽƬ�����֮��Ϊ ������ֱ��д���𰸣�
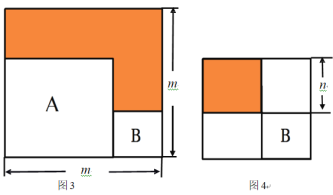
��3����ͼ2����A��B����������ֽƬ�����֮��Ϊ5����ͼ2����Ӱ���ֵ����Ϊ2������m��n��ֵ��

��4���ֽ�������ֽƬA��B���ŷ��ú����µ������ε�ͼ3����������ֽƬB����������ֽƬA���ڲ���ͼ4����ͼ3��ͼ4����Ӱ���ֵ�����ֱ�Ϊ12��1����A��B����������ֽƬ�����֮��Ϊ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���D�DZ�BC���е㣬��E����ABC�ڣ�AEƽ����BAC��CE��AE����F�ڱ�AB�ϣ�EF��BC��

��1����֤���ı���BDEF��ƽ���ı��Σ�
��2���߶�BF��AB��AC������֮����������Ĺ�ϵ��֤�������õ��Ľ��ۣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com