
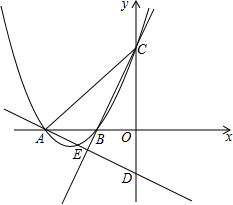
 如图,抛物线y=ax2+bx+6与x轴分别相交于点A、B,与y轴相交于点C,过点A的直线y=-$\frac{1}{2}$x+m与y轴相交于点D,连接CB并延长,与直线AD相交于点E,若点A的坐标为(-8,0),E为AD的中点,
如图,抛物线y=ax2+bx+6与x轴分别相交于点A、B,与y轴相交于点C,过点A的直线y=-$\frac{1}{2}$x+m与y轴相交于点D,连接CB并延长,与直线AD相交于点E,若点A的坐标为(-8,0),E为AD的中点,分析 (1)把A点坐标代入直线y=-$\frac{1}{2}$x+m,可求得m的值;
(2)由条件可先求得AC=CD=10,过B作BF⊥AC于点F,可得到BF=BO,在Rt△ABF中由勾股定理可求得BF,可求得B点坐标,再利用待定系数法可求得抛物线解析式;
(3)在直线AD的下方作∠EAQ=∠BAE,设CE的延长线与AQ相交于点G.直线AG与抛物线的交点就是所求的点P.由三角函数的定义可求得BE的长,过点E、G分别作EN⊥AB,GM⊥AB,垂足分别为N、M,可分别求得BN、EN,再根据△BEN∽△BGM可求得BM、MG,可求得G点坐标,可求得直线AG的解析式,则可求得P点坐标.
解答 解:
(1)∵直线y=-$\frac{1}{2}$x+m过A点,
∴把A点坐标代入可得0=-$\frac{1}{2}$×(-8)+m,解得m=-4,
故答案为:-4;
(2)抛物线y=ax2+bx+6,当x=0时,y=6.
∴OC=6.由题知OA=8.
∴AC=$\sqrt{O{A}^{2}+O{C}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10.
由(1)得,OD=4.
∴CD=10=CA.
∵AE=ED,
∴∠ACE=∠DCE.
如图1,过点B作BF⊥AC,垂足为F.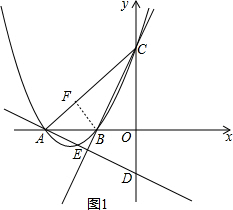
则CF=CO=6,BF=BO.
在Rt△ABF中,42+BF2=(8-BF)2.
∴BF=3=OB.即点B的坐标为(-3,0).
抛物线y=ax2+bx+6经过A(-8,0),B(-3,0),
则$\left\{\begin{array}{l}{64a-8b+6=0}\\{9a-3b+6=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=\frac{1}{4}}\\{b=\frac{11}{4}}\end{array}\right.$,
∴抛物线的解析式为y=$\frac{1}{4}$x2+$\frac{11}{4}$x+6;
(3)存在.
如图2,在直线AD的下方作∠EAQ=∠BAE,设CE的延长线与AQ相交于点G.直线AG与抛物线的交点就是所求的点P.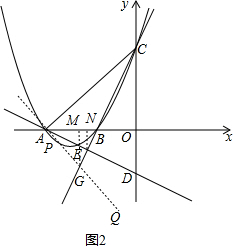
由(1)知,CE⊥AD,则BE=EG.
∵$\frac{BE}{AB}$=sin∠BAE=$\frac{OD}{AD}$,
∴BE=$\frac{OD•AB}{AD}$=$\frac{4×5}{4\sqrt{5}}$=$\sqrt{5}$.
过点E、G分别作EN⊥AB,GM⊥AB,垂足分别为N、M,则∠BEN=∠BAE.
∴BN=BE•sin∠BEN=$\sqrt{5}$×$\frac{\sqrt{5}}{5}$=1,EN=BE•cos∠BEN=$\sqrt{5}$×$\frac{2\sqrt{5}}{5}$=2.
∵EN∥GM,
∴△BEN∽△BGM.
∴$\frac{BN}{BM}$=$\frac{NE}{MG}$=$\frac{BE}{BG}$,即$\frac{1}{BM}$=$\frac{2}{MG}$=$\frac{1}{2}$.
∴BM=2,MG=4.
∴点G的坐标是(-5,-4).
设直线AG的解析式为y=kx+b,
则$\left\{\begin{array}{l}{-8k+b=0}\\{-5k+b=-4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-\frac{4}{3}}\\{b=-\frac{32}{3}}\end{array}\right.$,
∴直线AG的解析式为y=-$\frac{4}{3}$x-$\frac{32}{3}$.
根据题意,-$\frac{4}{3}$x-$\frac{32}{3}$=$\frac{1}{4}$x2+$\frac{11}{4}$x+6,解得x=-$\frac{25}{3}$或x=-8(舍去).
当x=-$\frac{25}{3}$时,y=-$\frac{4}{3}$×(-$\frac{25}{3}$)-$\frac{32}{3}$=$\frac{4}{9}$,
∴点P的坐标为(-$\frac{25}{3}$,$\frac{4}{9}$).
综上可知存在满足条件的点P,其坐标为(-$\frac{25}{3}$,$\frac{4}{9}$).
点评 本题主要考查二次函数的综合应用,涉及待定系数法、勾股定理、相似三角形的判定和性质、三角函数的定义等知识点.在(2)中求得BF=BO=3,得到B点坐标是解题的关键,在(3)中先确定出点P的位置,再求得G点坐标是解题的关键.本题考查知识点较多,综合性较强,计算量大,难度较大.


 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
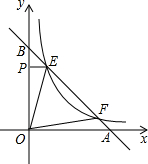 如图,点E、F在函数y=$\frac{k}{x}$(x>0)的图象上,直线EF分别与x轴、y轴交于点A、B,且BE:BF=1:4,过点E作EP⊥y轴于P,已知△OEP的面积为2.
如图,点E、F在函数y=$\frac{k}{x}$(x>0)的图象上,直线EF分别与x轴、y轴交于点A、B,且BE:BF=1:4,过点E作EP⊥y轴于P,已知△OEP的面积为2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:一个正比例函数和一个一次函数的图象交于点P(-2、2)且一次函数的图象与y轴的 交点Q的纵坐标为4.
已知:一个正比例函数和一个一次函数的图象交于点P(-2、2)且一次函数的图象与y轴的 交点Q的纵坐标为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
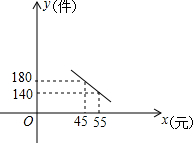 大学生王强积极响应“自主创业”的好种,准备投资销售一种进价为每件4元的小家电,通过试营销发现,当销售单价在40元至60元之间(含40元和60元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.
大学生王强积极响应“自主创业”的好种,准备投资销售一种进价为每件4元的小家电,通过试营销发现,当销售单价在40元至60元之间(含40元和60元)时,每月的销售量y(件)与销售单价x(元)之间的关系可近似地看作一次函数,其图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(元/个) | 30 | 40 | 50 |
| y(个) | 190 | 170 | 150 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,则点P3的坐标是(8,3);点P2015的坐标是(1,4).
如图,弹性小球从点P(0,3)出发,沿所示方向运动,每当小球碰到矩形OABC的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…,第n次碰到矩形的边时的点为Pn,则点P3的坐标是(8,3);点P2015的坐标是(1,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com