
【题目】(阅读理解)利用完全平方公式,可以将多项式![]() 变形为
变形为![]() 的形式,我们把这样的变形方法叫做多项式
的形式,我们把这样的变形方法叫做多项式![]() 的配方法.运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
的配方法.运用多项式的配方法及平方差公式能对一些多项式进行分解因式.
例如:![]()
![]()
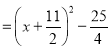
![]()
![]()
(问题解决)根据以上材料,解答下列问题:
(1)用多项式的配方法将多项式![]() 化成
化成![]() 的形式;
的形式;
(2)用多项式的配方法及平方差公式对多项式![]() 进行分解因式;
进行分解因式;
(3)求证:不论![]() ,
,![]() 取任何实数,多项式
取任何实数,多项式![]() 的值总为正数.
的值总为正数.
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】某中学举行“中国梦·校园好声音”歌手大赛,高、初中根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩(满分100)如下图所示:

根据图示信息,整理分析数据如下表:
平均数(分) | 中位数(分) | 众数(分) | |
初中部 |
| 85 |
|
高中部 | 85 |
| 100 |
(说明:图中虚线部分的间隔距离均相等)
(1)求出表格中![]() 的值;
的值;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差,并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边![]() 中,
中,![]() 厘米,
厘米,![]() 厘米,如果点
厘米,如果点![]() 以
以![]() 厘米
厘米![]() 的速度运动.
的速度运动.

(1)如果点![]() 在线段
在线段![]() 上由点
上由点![]() 向点
向点![]() 运动.点
运动.点![]() 在线段
在线段![]() 上由
上由![]() 点向
点向![]() 点运动,它们同时出发,若点
点运动,它们同时出发,若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度相等:
的运动速度相等:
①经过“![]() 秒后,
秒后,![]() 和
和![]() 是否全等?请说明理由.
是否全等?请说明理由.
②当两点的运动时间为多少秒时,![]() 刚好是一个直角三角形?
刚好是一个直角三角形?
(2)若点![]() 的运动速度与点
的运动速度与点![]() 的运动速度不相等,点
的运动速度不相等,点![]() 从点
从点![]() 出发,点
出发,点![]() 以原来的运动速度从点
以原来的运动速度从点![]() 同时出发,都顺时针沿
同时出发,都顺时针沿![]() 三边运动,经过
三边运动,经过![]() 秒时点
秒时点![]() 与点
与点![]() 第一次相遇,则点
第一次相遇,则点![]() 的运动速度是__________厘米
的运动速度是__________厘米![]() 秒.(直接写出答案)
秒.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近年来,安全快捷、平稳舒适的中国高铁,为世界高速铁路商业运营树立了新的标杆.随着中国特色社会主义进入新时代,作为“中国名片”的高速铁路也将踏上自己的新征程,跑出发展新速度,这就意味着今后外出旅行的路程与时间将大大缩短,但也有不少游客根据自己的喜好依然选择乘坐普通列车;已知从A地到某市的高铁行驶路程是400千米,普通列车的行驶路程是高铁行驶路程的1.3倍,请完成以下问题:
(1)普通列车的行驶路程为多少千米?
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需时间比乘坐普通列车所需时间缩短3小时,求普通列车和高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,矩形ABCD的顶点D在反比例函数![]() (x<0)的图象上,顶点B,C在x轴上,对角线AC的延长线交y轴于点E,连接BE,△BCE的面积是6,则k=_____.
(x<0)的图象上,顶点B,C在x轴上,对角线AC的延长线交y轴于点E,连接BE,△BCE的面积是6,则k=_____.
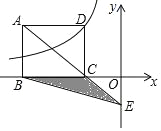
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1所示的遮阳伞,伞柄垂直于水平地面,其示意图如图2、当伞收紧时,点P与点A重合;当伞慢慢撑开时,动点P由A向B移动;当点P到达点B时,伞张得最开、已知伞在撑开的过程中,总有PM=PN=CM=CN=6.0分米,CE=CF=18.0分米,BC=2.0分米、设AP=x分米.
(1)求x的取值范围;
(2)若∠CPN=60°,求x的值;
(3)设阳光直射下,伞下的阴影(假定为圆面)面积为y,求y关于x的关系式(结果保留π).
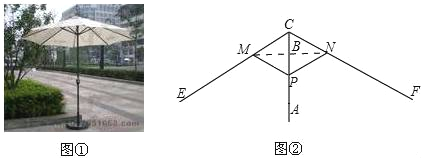
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在ABCD中,对角线AC,BD交于点O,AB⊥AC,AB=1,BC=![]() .
.
(1)求平行四边形ABCD的面积S□ABCD;
(2)求对角线BD的长.
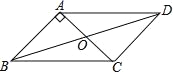
查看答案和解析>>
科目:初中数学 来源: 题型:
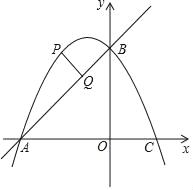
【题目】如图,在平面直角坐标系中,直线y=x+2与坐标轴交于A、B两点,点A在x轴上,点B在y轴上,C点的坐标为(1,0),抛物线y=ax2+bx+c经过点A、B、C.
(1)求该抛物线的解析式;
(2)根据图象直接写出不等式ax2+(b﹣1)x+c>2的解集;
(3)点P是抛物线上一动点,且在直线AB上方,过点P作AB的垂线段,垂足为Q点.当PQ=![]() 时,求P点坐标.
时,求P点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com