
【题目】如图,在Rt△ABC中,∠BAC=90°,∠B=60°,以边上AC上一点O为圆心,OA为半径作⊙O,⊙O恰好经过边BC的中点D,并与边AC相交于另一点F. 
(1)求证:BD是⊙O的切线;
(2)若BC=2 ![]() ,E是半圆
,E是半圆 ![]() 上一动点,连接AE、AD、DE. 填空:
上一动点,连接AE、AD、DE. 填空:
①当 ![]() 的长度是时,四边形ABDE是菱形;
的长度是时,四边形ABDE是菱形;
②当 ![]() 的长度是时,△ADE是直角三角形.
的长度是时,△ADE是直角三角形.
【答案】
(1)证明:连接OD,如图,
∵∠BAC=90°,点D为BC的中点,
∴DB=DA=DC,
∵∠B=60°,
∴△ABD为等边三角形,
∴∠DAB=∠ADB=60°,∠DAC=∠C=30°,
而OA=OD,
∴∠ODA=∠OAD=30°,
∴∠ODB=60°+30°=90°,
∴OD⊥BC,
∴BD是⊙O的切线;
(2)![]() π;
π;![]() π或π
π或π
【解析】(2)解:①∵△ABD为等边三角形, ∴AB=BD=AD=CD= ![]() ,
,
在Rt△ODC中,OD= ![]() CD=1,
CD=1,
当DE∥AB时,DE⊥AC,
∴AD=AE,
∵∠ADE=∠BAD=60°,
∴△ADE为等边三角形,
∴AD=AE=DE,∠ADE=60°,
∴∠AOE=2∠ADE=120°,
∴AB=BD=DE=AE,
∴四边形ABDE为菱形,
此时 ![]() 的长度=
的长度= ![]() =
= ![]() π;
π;
②当∠ADE=90°时,AE为直径,点E与点F重合,此时 ![]() 的长度=
的长度= ![]() =π;
=π;
当∠DAE=90°时,DE为直径,∠AOE=2∠ADE=60°,此时 ![]() 的长度=
的长度= ![]() =
= ![]() π,
π,
所以当 ![]() 的长度为
的长度为 ![]() π或π时,△ADE是直角三角形.
π或π时,△ADE是直角三角形.
故答案为 ![]() π;
π; ![]() π或π.
π或π.
(1)连接OD,如图,利用斜边上的中线性质得DB=DA=DC,则可判断△ABD为等边三角形得到∠DAB=∠ADB=60°,∠DAC=∠C=30°,然后计算出∠ODB=90°,从而根据切线的判定定理可判定BD是⊙O的切线;(2)解:①利用△ABD为等边三角形得到AB=BD=AD=CD= ![]() ,则可计算出OD=
,则可计算出OD= ![]() CD=1,当DE∥AB时,DE⊥AC,先证明△ADE为等边三角形,再证明四边形ABDE为菱形,然后利用弧长公式计算此时
CD=1,当DE∥AB时,DE⊥AC,先证明△ADE为等边三角形,再证明四边形ABDE为菱形,然后利用弧长公式计算此时 ![]() 的长度;②讨论:当∠ADE=90°时,AE为直径,利用弧长公式可计算出此时
的长度;②讨论:当∠ADE=90°时,AE为直径,利用弧长公式可计算出此时 ![]() 的长度;当∠DAE=90°时,DE为直径,利用圆周角定理得到∠AOE=2∠ADE=60°,然后利用弧长公式可计算出此时
的长度;当∠DAE=90°时,DE为直径,利用圆周角定理得到∠AOE=2∠ADE=60°,然后利用弧长公式可计算出此时 ![]() 的长度.
的长度.


 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,AC=BC,AB=4,D为AB上的动点,DP⊥AB交折线A﹣C﹣B于点P,设AD=x,△ADP的面积为y,则y与x的函数图象正确的是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校准备开展“阳光体育活动”,决定开设以下体育活动项目:足球、乒乓球、篮球和羽毛球,要求每位学生必须且只能选择一项,为了解选择各种体育活动项目的学生人数,随机抽取了部分学生进行调查,并将通过调查获得的数据进行整理,绘制出以下两幅不完整的统计图,请根据统计图回答问题: 
(1)这次活动一共调查了名学生;
(2)补全条形统计图;
(3)在扇形统计图中,选择篮球项目的人数所在扇形的圆心角等于度;
(4)若该学校有1500人,请你估计该学校选择足球项目的学生人数约是人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y= ![]() 在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( )
在第一象限的图象经过点B,则△OAC与△BAD的面积之差S△OAC﹣S△BAD为( ) 
A.36
B.12
C.6
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c(a≠0)经过A、B、C三点,点A、C的坐标分别是(0,4)、(﹣1,0).
(1)求此抛物线的解析式;
(2)点P是第一象限内抛物线上的一动点,当△ABP的面积最大时,求出此时P的坐标及面积的最大值;
(3)若G为抛物线上的一动点,F为x轴上的一动点,点D坐标为(1,4),点E坐标为(1,0),当D、E、F、G构成平行四边形时,请直接写出点G的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个点在第一象限及x轴、y轴上运动,且每秒移动一个单位,在第1秒钟,它从原点运动到(0,1),然后接着按图中箭头所示方向运动[即(0,0)→(0,1)→(1,1)→(1,0)→…],那么第35秒时质点所在位置的坐标是( ) 
A.(4,0)
B.(0,5)
C.(5,0)
D.(5,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,⊙M与x轴相切于点A(8,0),与y轴分别交于点B(0,4)和点C(0,16),则圆心M到坐标原点O的距离是( ) 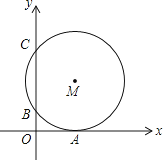
A.10
B.8 ![]()
C.4 ![]()
D.2 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com