【题目】如图，反比例函数y= 与一次函数y=ax+b的图象交于点A（2，2）、B（ ，n）．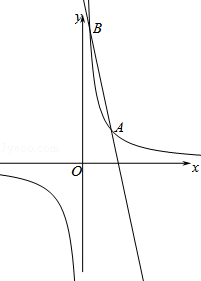
（1）求这两个函数解析式；
（2）将一次函数y=ax+b的图象沿y轴向下平移m个单位，使平移后的图象与反比例函数y= 的图象有且只有一个交点，求m的值．

参考答案：

【答案】
（1）解：∵A（2，2）在反比例函数 的图象上，

∴k=4．

∴反比例函数的解析式为 ．

又∵点B（ ，n）在反比例函数 的图象上，

∴ ，解得：n=8，

即点B的坐标为（ ，8）．

由A（2，2）、B（ ，8）在一次函数y=ax+b的图象上，

得： ，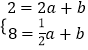

解得： ，

∴一次函数的解析式为y=﹣4x+10


（2）解：将直线y=﹣4x+10向下平移m个单位得直线的解析式为y=﹣4x+10﹣m，

∵直线y=﹣4x+10﹣m与双曲线 有且只有一个交点，

令 ，得4x2+（m﹣10）x+4=0，

∴△=（m﹣10）2﹣64=0，

解得：m=2或m=18


【解析】（1）由点A在反比例函数的图象上，结合反比例函数图象上的点的坐标特征即可得出反比例函数的解析式；由点B的横坐标以及反比例函数的解析式即可得出点B的坐标，再由A、B点的坐标利用待定系数法即可求出一次函数得解析式；（2）结合（1）中得结论找出平移后的直线的解析式，将其代入反比例函数解析式中，整理得出关于x的二次方程，令其根的判别式△=0，即可得出关于m的一元二次方程，解方程即可得出结论．

关闭