
【题目】(1)如图,已知点C在线段AB上,AC=6cm,且BC=4cm,M、N分别是AC、BC的中点,求线段MN的长度;
![]()
(2)在(1)题中,如果![]() 其他条件不变,你能猜出MN的长度吗?请你用一句简洁的话表达你发现的规律;
其他条件不变,你能猜出MN的长度吗?请你用一句简洁的话表达你发现的规律;
(3)对于(1)题,当点C在BA的延长线上时,且AB=![]() 其他条件不变,求MN的长度.
其他条件不变,求MN的长度.
【答案】(1)5cm;(2)见解析;(3) ![]() .
.
【解析】
(1)根据线段中点的性质,可得MC、NC的长,根据线段的和差,可得答案;
(2)根据线段中点的性质,可得MC、NC的长,根据线段的和差,可得答案;(3) 根据线段中点的性质,可得MC、NC的长,根据BC=AB+AC,可得MN=![]() .
.
(1)解:因为M,N分别是AC,BC的中点所以,
MC=![]() AC=
AC=![]() ×6=3cm,
×6=3cm,
NC=![]() BC=
BC=![]() ×4=2cm,
×4=2cm,
所以,MN=MC+NC=3+2=5(cm);
(2)解:由(1)知MC=![]() a,NC=
a,NC=![]() b,
b,
所以,MN=MC+NC=![]() a+
a+![]() b=
b=![]() (a+b).
(a+b).
规律:直线上相邻两线段中点间的距离为两线段长度和的一半.
(3) 当点C在线段BA的延长线时,如图:![]()
因为M,N分别是AC,BC的中点所以,
CM=![]() AC
AC
CN=![]() BC
BC
∴MN=CN-CM=![]() ,
,
∵BC=AB+AC,AB=m,
∴MN=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
【题目】某校九年级开展“光盘行动”宣传活动,各班级参加该活动的人数统计结果如下表,对于这组统计数据,下列说法中正确的是( )
班级 | 1班 | 2班 | 3班 | 4班 | 5班 | 6班 |
人数 | 52 | 60 | 62 | 54 | 58 | 62 |
A.平均数是58
B.中位数是58
C.极差是40
D.众数是60
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老师想知道学生们每天在上学的路上要花多少时间,于是让大家将每天来校上课的单程时间写在纸上.下面是全班30名学生单程所花的时间(单位:min):
20,20,30,15,20,25,5,15,20,10,15,35,45,10,20,25,30,20,15,20,20,10,20,5,15,20,20,20,5,15.
(1)用表格将上述数据加以整理;
(2)画出学生上学单程所花时间与次数的条形统计图;
(3)根据调查结果,计算每天单程20min到校的学生有多少名?占全班学生人数的百分比是多少?你认为老师还能获得哪些信息?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(a-b)2(a-b)3(b-a)5 (2)(a-b+c)3(b-a-c)5(a-b+c)6
(3)(b-a)m·(b-a)n-5·(a-b)5 (4)x·xm-1+x2·xm-2-3x3·xm-3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC 三个顶点的坐标分别为 A(1,1),B(4,2),C(3,4).
(1)请画出△ABC 向左平移 5 个单位长度后得到的△A1B1C1;
(2)在 x 轴上求作一点 P,使△PAB 的周长最小,请画出△PAB,并直接写出 P 的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点C(0,4)与x轴交于点A、B,点B(4,0),抛物线的对称轴为x=1.直线AD交抛物线于点D(2,m).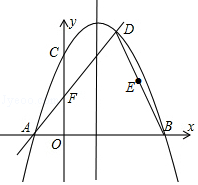
(1)求二次函数的解析式并写出D点坐标;
(2)点E是BD的中点,点Q是线段AB上一动点,当△QBE和△ABD相似时,求点Q的坐标;
(3)抛物线与y轴交于点C,直线AD与y轴交于点F,点M为抛物线对称轴上的动点,点N在x轴上,当四边形CMNF周长取最小值时,求出满足条件的点M和点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上A 点对应的数为﹣5,B 点在A 点右边,电子蚂蚁甲、乙在B分别以2个单位/秒、1个单位/秒的速度向左运动,电子蚂蚁丙在A 以3个单位/秒的速度向右运动.
(1)若电子蚂蚁丙经过5秒运动到C 点,求C 点表示的数;
![]()
(2)若它们同时出发,若丙在遇到甲后1秒遇到乙,求B 点表示的数;
![]()
(3)在(2)的条件下,设它们同时出发的时间为t 秒,是否存在t的值,使丙到乙的距离是丙到甲的距离的2倍?若存在,求出t 值;若不存在,说明理由.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,填空:
(1)若∠4=∠3,则____∥_____,理由是______;
(2)若∠2=∠E,则____∥___,理由是____;
(3)若∠A=∠ABE=180°,则____∥___,理由是____;
(4)若∠2=∠____,则DA∥EB,理由是____;
(5)若∠DBC+∠_____=180°,则DB∥EC,理由是____;

查看答案和解析>>
科目:初中数学 来源: 题型:
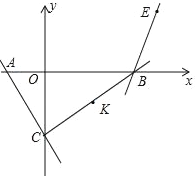
【题目】如图,在平面直角坐标系中,直线y=﹣![]() x﹣
x﹣![]() 交x轴于点A,交y轴于点C,直线y=
交x轴于点A,交y轴于点C,直线y=![]() x﹣5
x﹣5![]() 交x轴于点B,在平面内有一点E,其坐标为(4,
交x轴于点B,在平面内有一点E,其坐标为(4,![]() ),连接CB,点K是线段CB的中点,另有两点M,N,其坐标分别为(a,0),(a+1,0).将K点先向左平移
),连接CB,点K是线段CB的中点,另有两点M,N,其坐标分别为(a,0),(a+1,0).将K点先向左平移![]() 个单位,再向上平移
个单位,再向上平移![]() 个单位得K′,当以K′,E,M,N四点为顶点的四边形周长最短时,a的值为_____.
个单位得K′,当以K′,E,M,N四点为顶点的四边形周长最短时,a的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com