
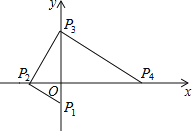
【题目】如图,点P1,P2,P3,P4均在坐标轴上,且P1P2⊥P2P3,P2P3⊥P3P4,若点P1,P2的坐标分别为(0,﹣1),(﹣2,0),求点P4的坐标.
科目:初中数学 来源: 题型:
【题目】抛物线![]() 经过点A(-4,0),B(2,0)且与
经过点A(-4,0),B(2,0)且与![]() 轴交于点C.
轴交于点C.
(1)求抛物线的解析式;
(2)如图1,P为线段AC上一点,过点P作![]() 轴平行线,交抛物线于点D,当△ADC的面积最大时,求点P的坐标;
轴平行线,交抛物线于点D,当△ADC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴子F点,M、N分别是![]() 轴和线段EF上的动点,设M的坐标为(m,0),若∠MNC=90°,请指出实数m的变化范围,并说明理由.
轴和线段EF上的动点,设M的坐标为(m,0),若∠MNC=90°,请指出实数m的变化范围,并说明理由.
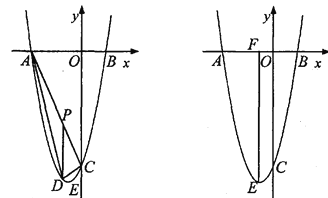
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】嘉淇同学要证明命题“两组对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图所示的四边形ABCD,并写出了如下不完整的已知和求证.已知:如图,在四边形ABCD中,BC=AD,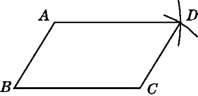
AB=__①___.
求证:四边形ABCD是___②___四边形.
(1)在方框中填空,以补全已知和求证;
①;②.
(2)按嘉淇的想法写出证明.
(3)用文字叙述所证命题的逆命题为
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】标号为A、B、C、D的四个盒子中所装有白球和黑球数如下,则下列盒子最易摸到黑球的是( )
A.9个黑球和3个白球 B.10黑球和10个白球
C.12个黑球和6个白球 D.10个黑球和5个白球
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠BCA=90°,AC=BC,点D是BC的中点,点F在线段AD上,DF=CD,BF交CA于E点,过点A作DA的垂线交CF的延长线于点G,下列结论:①CF2=EFBF;②AG=2DC;③AE=EF;④AFEC=EFEB.其中正确的结论有________
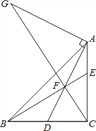
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,边长为a的正方形ABCD和边长为b的正方形BEFG排放在一起,O1和O2分别是两个正方形的中心,则阴影部分的面积为 , 线段O1O2的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AF、CE分别是∠BAD和∠BCD的角平分线,根据现有的图形,请添加一个条件,使四边形AECF为菱形,则添加的一个条件可以是 . (只需写出一个即可,图中不能再添加别的“点”和“线”)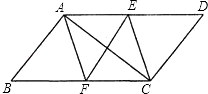
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,点P的坐标为(﹣5,3),则点P关于原点对称的点的坐标是( )
A. (5,﹣3) B. (﹣5,﹣3) C. (3,﹣5) D. (﹣3,5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com