
【题目】抛物线![]() 经过点A(-4,0),B(2,0)且与
经过点A(-4,0),B(2,0)且与![]() 轴交于点C.
轴交于点C.
(1)求抛物线的解析式;
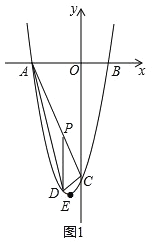
(2)如图1,P为线段AC上一点,过点P作![]() 轴平行线,交抛物线于点D,当△ADC的面积最大时,求点P的坐标;
轴平行线,交抛物线于点D,当△ADC的面积最大时,求点P的坐标;
(3)如图2,抛物线顶点为E,EF⊥x轴子F点,M、N分别是![]() 轴和线段EF上的动点,设M的坐标为(m,0),若∠MNC=90°,请指出实数m的变化范围,并说明理由.
轴和线段EF上的动点,设M的坐标为(m,0),若∠MNC=90°,请指出实数m的变化范围,并说明理由.
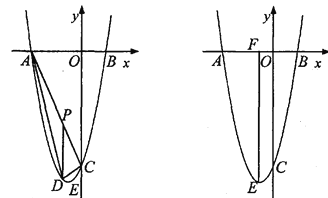
图1 图2
【答案】(1)y=x2+2x﹣8;(2)(﹣2,﹣4);(3)﹣10≤m≤15
【解析】试题分析:(1)只需用待定系数法就可求出抛物线的解析式;
(2)可用待定系数法求出直线AC的解析式为y=-2x-8,设点P的坐标为(a,-2a-8),则点D(a,a2+2a-8),(-4<a<0),然后用割补法求得S△ADC=-2(a+2)2+8,从而可求出△ADC的面积最大时点P的坐标;
(3)易求得OF=1、EF=9、OC=8.设FN=n,(0≤n≤9),然后分三种情况(Ⅰ.M与点F重合,Ⅱ.M在点F左侧,Ⅲ.M在点F右侧)讨论,运用相似三角形的性质均可得到m=-n2+8n-1(0≤n≤9).由m=-n2+8n-1=-(n-4)2+15可得到m最大值为15,再由n=0时m=-1,n=9时m=-10可得m最小值为-10,从而可得到m的取值范围.
解:(1)∵抛物线y=x2+bx+c经过点A(﹣4,0),B(2,0),
∴![]() ,
,
解得![]() .
.
∴抛物线的解析式为y=x2+2x﹣8.
(2)如图1,
令x=0,得y=﹣8,
∴点C的坐标为(0,﹣8).
设直线AC的解析式为y=kx+t,
则![]() ,
,
解得:![]() ,
,
∴直线AC的解析式为y=﹣2x﹣8.
设点P的坐标为(a,﹣2a﹣8),则点D(a,a2+2a﹣8),(﹣4<a<0),
∴PD=(﹣2a﹣8)﹣(a2+2a﹣8)=﹣a2﹣4a,
∴S△ADC=S△APD+S△CPD
=![]() PD[a﹣(﹣4)]+
PD[a﹣(﹣4)]+![]() PD(0﹣a)
PD(0﹣a)
=2PD=﹣2(a2+4a)
=﹣2(a+2)2+8,
∴当a=﹣2时,S△ADC取到最大值为8,此时点P的坐标为(﹣2,﹣4).
(3)由y=x2+2x﹣8=(x+1)2﹣9得E(﹣1,﹣9)、C(0,﹣8),
则有OF=1、EF=9、OC=8.
设FN=n,(0≤n≤9),
Ⅰ.当M与点F重合时,此时m=﹣1,n=8,显然成立;
Ⅱ.当M在点F左侧,作NQ⊥y轴于点Q,如图2①,此时m<﹣1.

∵∠MNC=∠FNQ=90°,∴∠MNF=∠CNQ.
∵∠MFN=∠CQN=90°,
∴△MFN∽△CQN,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴m=﹣n2+8n﹣1.
Ⅲ.当M在点F右侧,作NQ′⊥y轴于点Q′,如图2②,此时m>﹣1.

∵∠MNC=∠FNQ′=90°,∴∠MNF=∠CNQ′.
∵∠MFN=∠CQ′N=90°,
∴△MFN∽△CQ′N,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴m=﹣n2+8n﹣1.
综上所述:m=﹣n2+8n﹣1,(0≤n≤9).
∴m=﹣n2+8n﹣1=﹣(n﹣4)2+15,
∴当n=4时,m取到最大值为15.
∵n=0时m=﹣1,n=9时m=﹣10,
∴m取到最小值为﹣10,
∴m的取值范围是﹣10≤m≤15.


科目:初中数学 来源: 题型:
【题目】NBA季后赛正如火如荼地进行着,詹姆斯率领的骑士队在第三场季后赛中先落后25分的情况
下实现了大逆转.该场比赛中詹姆斯的技术统计数据如下表所示:
技术 | 上场时间 (分钟) | 出手投篮(次) | 投中 (次) | 罚球 得分 | 篮板 (个) | 助攻 (次) | 个人 总得分 |
数据 | 45 | 27 | 14 | 7 | 13 | 12 | 41 |
【注:表中出手投篮次数和投中次数均不包括罚球,个人总得分来自2分球和3分球的得分以及罚
球得分.】根据以上信息,求出本场比赛中詹姆斯投中2分球和3分球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
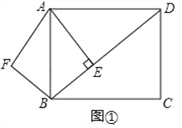
【题目】已知:如图①,在矩形ABCD中,AB=5,AD=![]() ,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
,AE⊥BD,垂足是E.点F是点E关于AB的对称点,连接AF、BF.
(1)求AE和BE的长;
(2)若将△ABF沿着射线BD方向平移,平移中的△ABF为△A1B1F1设平移的距离为m(平移距离指点B沿BD方向所经过的线段长度).
①当点F分别平移到线段AB上时,求出m的值
②当点F分别平移到线段AD上时,当直接写出相应的m的值.
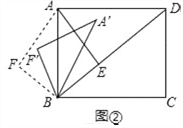
(3)如图②,将△ABF绕点B顺时针旋转一个角α(0°<α<180°),记旋转中的△ABF为△A′BF′,在旋转过程中,设A′F′所在的直线与直线AE交于点O,当∠A′BD=∠FAB时,请直接写出OB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以扇形OAB的顶点O为原点,半径OB所在的直线为![]() 轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线
轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线![]() 与扇形OAB的边界总有两个公共点,则实数
与扇形OAB的边界总有两个公共点,则实数![]() 的取值范围是________________.
的取值范围是________________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了满足学生借阅图书的需求,计划购买一批新书,为此,该校图书管理员对一周内本校学生从图书馆借出各类图书的数量进行了统计,结果如图所示
请你根据统计图中的信息,解答下列问题: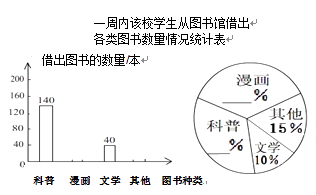
(1)补全条形统计图和扇形统计图
(2)该校学生最喜欢借阅哪类图书?并求出此类图书所在扇形的圆心角的度数?
(3)该校计划购买新书共600本,若按扇形统计图中的百分比来相应地确定漫画、科普、文学、其他这四类图书的购买量,问应购买这四类图书各多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,线段A′B′是由线段AB经过平移得到的,已知点A(﹣2,1)的对应点为A′(3,﹣1),点B的对应点为B′(4,0),则点B的坐标为( )
A.(9,﹣1)
B.(﹣1,0)
C.(3,﹣1)
D.(﹣1,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题
几个人共同种-批树苗,如果每个人种8棵,则剩余5棵树苗未种;如果增加3棵树苗,则每个人刚好种10棵树苗.求原有多少棵树苗和多少个人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P1,P2,P3,P4均在坐标轴上,且P1P2⊥P2P3,P2P3⊥P3P4,若点P1,P2的坐标分别为(0,﹣1),(﹣2,0),求点P4的坐标.
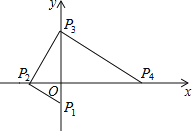
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com