
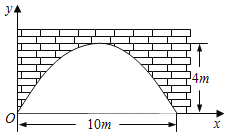
【题目】有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m,如图所示,把它的图形放在直角坐标系中.
(1)求这条抛物线所对应的函数关系式;
(2)一辆宽为2米,高为3米的货船能否从桥下通过?
【答案】(1)抛物线解析式为y=﹣![]() x2+
x2+![]() x;(2)货船能从桥下通过.
x;(2)货船能从桥下通过.
【解析】
(1)根据题意确定抛物线顶点坐标,利用待定系数法求函数解析式;(2)由抛物线对称轴直线x=5分析,船宽2米时,计算x=6是函数值是否大于3即可求解.
(1)根据题意,得
抛物线的顶点坐标为(5,4),经过(0,0),
∴设:抛物线解析式为y=a(x﹣5)2+4,
把(0,0)代入,得
25a+4=0,解得a=![]() ,
,
所以抛物线解析式为:y=![]() (x﹣5)2+4=
(x﹣5)2+4=![]() x2+
x2+![]() x.
x.
(2)货船能从桥下通过.理由如下:
由(1)可知,抛物线对称轴为直线x=5,又∵货船宽为2米,高为3米,
∴当x=6时,y=![]() (6﹣5)2+4=3.84,
(6﹣5)2+4=3.84,
∵3.84>3,
∴货船能从桥下通过.
答:货船能从桥下通过.


 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
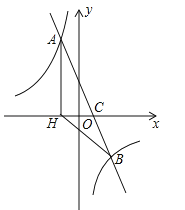
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数![]() (k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=
(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=![]() ,cos∠ACH=
,cos∠ACH=![]() ,点B的坐标为(4,n)
,点B的坐标为(4,n)
(1)求该反比例函数和一次函数的解析式;
(2)求△BCH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
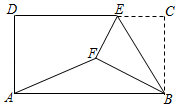
【题目】如图,在矩形ABCD中,AB=4,BC=![]() ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=
,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=![]() ,则CE=_____.
,则CE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, 抛物线![]() 与
与![]() 轴交于点A(-1,0),顶点坐标(1,n)与
轴交于点A(-1,0),顶点坐标(1,n)与![]() 轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①
轴的交点在(0,2),(0,3)之间(包 含端点),则下列结论:①![]() ;②
;②![]() ;③对于任意实数m,
;③对于任意实数m,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 有两个不相等的实数根.其中结论正确的个数为
有两个不相等的实数根.其中结论正确的个数为![]()
![]()

A. 1 个 B. 2 个 C. 3 个 D. 4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3(a≠0)经过A(3,0),B(4,1)两点,且与y轴交于点C.
(1)求抛物线y=ax2+bx+3(a≠0)的函数关系式及点C的坐标;
(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求点E的坐标.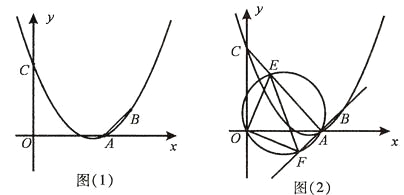
查看答案和解析>>
科目:初中数学 来源: 题型:
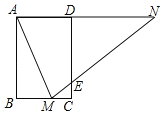
【题目】如图,矩形ABCD中,AB=3,BC=2,点M在BC上,连接AM,作∠AMN=∠AMB,点N在直线AD上,MN交CD于点E.
(1)求证:△AMN是等腰三角形;
(2)求证:AM2=2BMAN;
(3)当M为BC中点时,求ME的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】高尔基说:“书,是人类进步的阶梯. ”阅读可以丰富知识、拓展视野、充实生活等诸多益处. 为了解学生的课外阅读情况,某校随机抽查了部分学生阅读课外书册数的情况,并绘制出如下统计图,其中条形统计图因为破损丢失了阅读5册书数的数据.
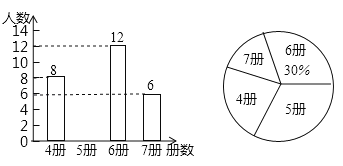
(1)条形图中丢失的数据是 ,并写出阅读书册数的众数是 、中位数是 ;
(2)根据随机抽查的这个结果,估计该校1200名学生中课外阅读5册书的学生人数是 ;
(3)若学校又补查了部分同学的课外阅读情况,得知这部分同学中课外阅读最少的是6册,将补查的情况与之前的数据合并后发现中位数并没有改变,试求最多补查了多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
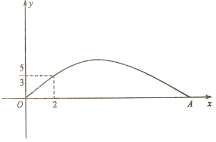
【题目】在某场足球比赛中,球员甲在球门正前方点O处起脚射门,在不受阻挡的情况下,足球沿如图所示的抛物线飞向球门中心线,当足球飞行的水平距离为2 m时,高度为![]() ,落地点A距O点12 m.已知点O距球门9 m,球门的横梁高为2.44 m.
,落地点A距O点12 m.已知点O距球门9 m,球门的横梁高为2.44 m.
(1)飞行的足球能否射入球门?通过计算说明理由;
(2)若守门员乙站在球门正前方2 m处,他跳起时能摸到的最大高度为2.52 m,他能阻止此次射门吗?并写明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成相应的任务:
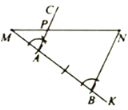
我们知道,利用尺规作已知线段的垂直平分线可以得到该线段的中点、四等分点、……怎样得到线段的三等分点呢?如图,已知线段MN,用尺规在MN上求作点P,使![]() .
.
小颖的作法是:
①作射线MK(点K不在直线MN上);
②在射线MK上依次截取线段MA,AB,使![]() ,连接BN;
,连接BN;
③作射线![]() ,交MN于点P点P即为所求作的点.
,交MN于点P点P即为所求作的点.
小颖作法的理由如下:
∵![]() (作法),∴
(作法),∴![]()
∵![]() (已知),
(已知),![]() (等量代换)
(等量代换)
∵![]() (线段和差定义),∴
(线段和差定义),∴![]() (等量代换,等式性质)
(等量代换,等式性质)
数学思考:(1)小颖作法理由中所缺的依据是:________________________________.
拓展应用:(2)如图,已知线段a,b,c,求作线段d,使![]()
a. ![]() b.
b. ![]() c.
c. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com