
【题目】已知抛物线y=ax2+bx+3(a≠0)经过A(3,0),B(4,1)两点,且与y轴交于点C.
(1)求抛物线y=ax2+bx+3(a≠0)的函数关系式及点C的坐标;
(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
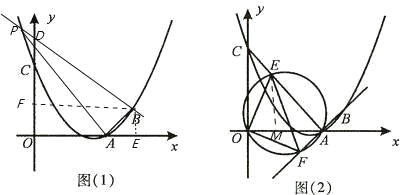
(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求点E的坐标.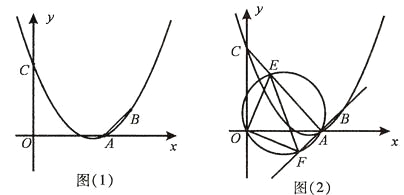
【答案】:(1)(0,3);
(2)点P的坐标为:(﹣1,6),(4,﹣1),(0,3);
(3)E点坐标为![]() .
.
【解析】
(1)根据A(3,0),B(4,1)两点利用待定系数法求二次函数解析式;
(2)从当△PAB是以AB为直角边的直角三角形,且∠PAB=90°与当△PAB是以AB为直角边的直角三角形,且∠PBA=90°,分别求出符合要求的答案;
(3)根据当OE∥AB时,△FEO面积最小,得出OM=ME,求出即可.
解:(1)∵抛物线y=ax2+bx+3(a≠0)经过A(3,0),B(4,1)两点,
∴![]() ,
,
解得: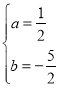 ,
,
∴![]() ;
;
∴点C的坐标为:(0,3);
(2)当△PAB是以AB为直角边的直角三角形,且∠PAB=90°,
∵A(3,0),B(4,1),
∴AM=BM=1,
∴∠BAM=45°,
∴∠DAO=45°,
∴AO=DO,
∵A点坐标为(3,0),
∴D点的坐标为:(0,3),
∴直线AD解析式为:y=kx+b,将A,D分别代入得:
∴0=3k+b,b=3,
∴k=﹣1,
∴y=﹣x+3,
∴![]() ,
,
∴x2﹣3x=0,
解得:x=0或3,
∴y=3或0(不合题意舍去),
∴P点坐标为(0,3),
当△PAB是以AB为直角边的直角三角形,且∠PBA=90°,
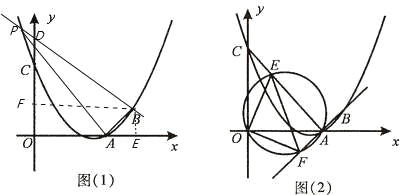
由(1)得,FB=4,∠FBA=45°,
∴∠DBF=45°,∴DF=4,
∴D点坐标为:(0,5),B点坐标为:(4,1),
∴直线AD解析式为:y=kx+b,将B,D分别代入得:
∴1=4k+b,b=5,
∴k=﹣1,
∴y=﹣x+5,
∴![]() ,
,
∴x2﹣3x﹣4=0,
解得:x1=﹣1,x2=4,
∴y1=6,y2=1,
∴P点坐标为(﹣1,6),(4,﹣1)
∵P(4,﹣1)与点B重合,故舍去
∴点P的坐标为:(﹣1,6),(0,3);
(3)作EM⊥BO,
∵当OE∥AB时,△FEO面积最小,
∴∠EOM=45°,
∴MO=EM,
∵E在直线CA上,
∴E点坐标为(x,﹣x+3),
∴x=﹣x+3,
解得:![]() ,
,
∴E点坐标为![]() .
.


科目:初中数学 来源: 题型:
【题目】一块材料的形状是锐角三角形ABC,边BC=120mm,高4D=80mm, .把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
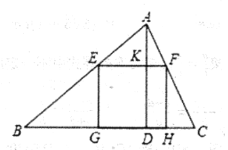
(1)求证:![]() ;
;
(2)求这个正方形零件的边长;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在小正方形构成的网格中,每个小正方形的顶点叫做格点.
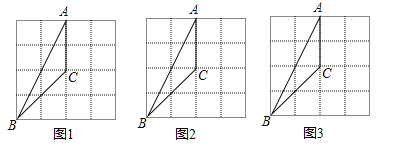
(1)![]() 的三个顶点都在格点上.
的三个顶点都在格点上.
①在图1中,画出一个与![]() 成中心对称的格点三角形;
成中心对称的格点三角形;
②在图2中,画出一个与![]() 成轴对称且与
成轴对称且与![]() 有公共边的格点三角形;
有公共边的格点三角形;
③在图3中,画出![]() 绕着点
绕着点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 后的三角形.
后的三角形.
(2)如图4是由5个边长为1的小正方形拼成的图形,请选择适当的格点,用无刻度的直尺面经过点![]() 的一条直线,使它平分该图形的面积,保留连线的痕迹,不要求说明理由.
的一条直线,使它平分该图形的面积,保留连线的痕迹,不要求说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
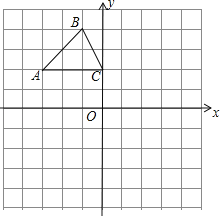
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(﹣3,2),B(﹣1,4),C(0,2).
(1)请画出△ABC关于点O的对称图形△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得到△A2B2C2,请画出△A2B2C2并求出在旋转过程中点B所经过的圆弧长.
查看答案和解析>>
科目:初中数学 来源: 题型:
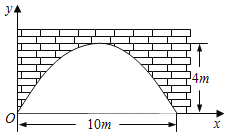
【题目】有一个抛物线形的拱形桥洞,桥洞离水面的最大高度为4m,跨度为10m,如图所示,把它的图形放在直角坐标系中.
(1)求这条抛物线所对应的函数关系式;
(2)一辆宽为2米,高为3米的货船能否从桥下通过?
查看答案和解析>>
科目:初中数学 来源: 题型:
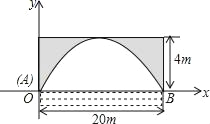
【题目】有一座抛物线形拱桥,正常水位时桥下水面宽为20m,拱顶距水面4m.
(1)在如图的直角坐标系中,求出该抛物线的解析式;
(2)为保证过往船只顺利航行,桥下水面宽度不得小于18m,求水面在正常水位基础上,最多涨多少米,不会影响过往船只?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com