
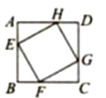
【题目】如图,正方形EFGH的四个顶点分别在正方形ABCD的四条边上,若正方形EFGH与正方形ABCD的相似比为![]() ,则
,则![]() (
(![]() )的值为_____.
)的值为_____.
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3(a≠0)经过A(3,0),B(4,1)两点,且与y轴交于点C.
(1)求抛物线y=ax2+bx+3(a≠0)的函数关系式及点C的坐标;
(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求点E的坐标.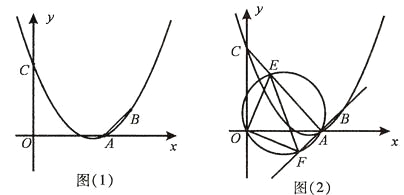
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量重庆有名的观景点南山大金鹰的大致高度,小南同学使用的无人机进行观察,当无人机与大金鹰侧面在同一平面,且距离水平面垂直高度GF为100米时,小南调整摄像头方向,当俯角为45°时,恰好可以拍摄到金鹰的头顶A点;当俯角为63°时,恰好可以拍摄到金鹰底座点E.已知大金鹰是雄踞在一人造石台上,石台侧面CE长12.5米,坡度为1:0.75,石台上方BC长10米,头部A点位于BC中点正上方.则金鹰自身高度约( )米.(结果保留一位小数,sin63°≈0.89,cos63°≈0.45,tan63°≈1.96)
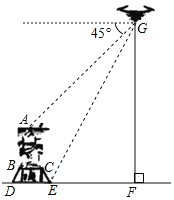
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
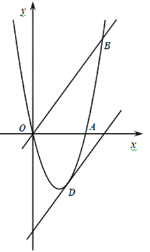
【题目】如图:已知抛物线y=ax2+bx(a≠0)经过A(3,0),B(4,4)两点.
(1)求抛物线解析式.
(2)将直线OB向下平移m个单位后,得到的直线与抛物线只有一个公共点D,求m值及交点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解方程。
(1)4(x-3) ![]() =36
=36
(2)x2-4x+1=0.
(3)![]() -7x+6=0
-7x+6=0
(4)![]()
(5)(y-1)2+2y(1-y)=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,完成相应的任务:
我们知道,利用尺规作已知线段的垂直平分线可以得到该线段的中点、四等分点、……怎样得到线段的三等分点呢?如图,已知线段MN,用尺规在MN上求作点P,使![]() .
.
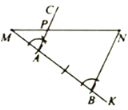
小颖的作法是:
①作射线MK(点K不在直线MN上);
②在射线MK上依次截取线段MA,AB,使![]() ,连接BN;
,连接BN;
③作射线![]() ,交MN于点P点P即为所求作的点.
,交MN于点P点P即为所求作的点.
小颖作法的理由如下:
∵![]() (作法),∴
(作法),∴![]()
∵![]() (已知),
(已知),![]() (等量代换)
(等量代换)
∵![]() (线段和差定义),∴
(线段和差定义),∴![]() (等量代换,等式性质)
(等量代换,等式性质)
数学思考:(1)小颖作法理由中所缺的依据是:________________________________.
拓展应用:(2)如图,已知线段a,b,c,求作线段d,使![]()
a. ![]() b.
b. ![]() c.
c. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市以20元/千克的进货价购进了一批绿色食品,如果以30元/千克销售这些绿色食品,那么每天可售出400千克.由销售经验可知,每天的销售量y(千克)与销售单价x(元)(x≥30)存在如图所示的一次函数关系.
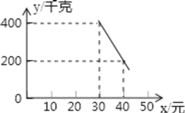
(1)试求出y与x的函数关系式;
(2)设该超市销售该绿色食品每天获得利润w元,当销售单价为何值时,每天可获得最大利润?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
(3)如果点D(a,b)在线段AB上,请直接写出经过(2)的变化后D的对应点D2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的解析式是y=x2﹣2x﹣3.
(1)与y轴的交点坐标是 ,顶点坐标是 .
(2)在坐标系中利用描点法画出此抛物线;
x | … | … | |||||
y | … | … |
(3)结合图象回答:当﹣2<x<2时,函数值y的取值范围是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com