
【题目】一块材料的形状是锐角三角形ABC,边BC=120mm,高4D=80mm, .把它加工成正方形零件如图1,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.
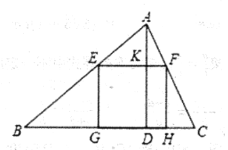
(1)求证:![]() ;
;
(2)求这个正方形零件的边长;
 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】现有甲、乙、丙三人组成的篮球训练小组,他们三人之间进行互相传球练习,篮球从一个人手中随机传到另外一个人手中计作传球一次,共连续传球三次.
(1)若开始时篮球在甲手中,则经过第一次传球后,篮球落在丙的手中的概率是 ;
(2)若开始时篮球在甲手中,求经过连续三次传球后,篮球传到乙的手中的概率.(请用画树状图或列表等方法求解)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C(0,3).
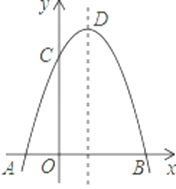
(1)求此抛物线所对应函数的表达式;
(2)若M 是抛物线对称轴上一个动点,求当 MA+MC 的值最小时 M 点坐标;
(3)若抛物线的顶点为D,在其对称轴右侧的抛物线上是否存在点P,使得△PCD为等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班学生做“用频率估计概率”的实验时,给出的某一结果出现的频率折线图,则符合这一结果的实验可能是( )
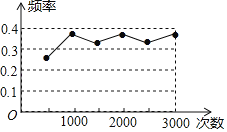
A.抛一枚硬币,出现正面朝上
B.从标有1,2,3,4,5,6的六张卡片中任抽一张,出现偶数
C.从一个装有6个红球和3个黑球的袋子中任取一球,取到的是黑球
D.一副去掉大小王的扑克牌洗匀后,从中任抽一张牌的花色是红桃
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市茶叶专卖店销售某品牌茶叶,其进价为每千克 240 元,按每千克 400 元出售,平均每周可售出 200 千克,后来经过市场调查发现,单价每降低 10 元,则平均每周的销售量可增加 40 千克,若该专卖店销售这种品牌茶叶要想平均每周获利 41600 元,请回答:
(1)每千克茶叶应降价多少元?
(2)在平均每周获利不变的情况下,为尽可能让利于顾客,赢得市场,该店应按原售价的 几折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
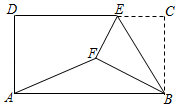
【题目】如图,在矩形ABCD中,AB=4,BC=![]() ,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=
,E为CD边上一点,将△BCE沿BE折叠,使得C落到矩形内点F的位置,连接AF,若tan∠BAF=![]() ,则CE=_____.
,则CE=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 垂直平分
垂直平分![]()
![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;同时,点
;同时,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;当一个点停止运动,另一个点也停止运动.过点
;当一个点停止运动,另一个点也停止运动.过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .连接
.连接![]() ,
,![]() .设运动时间为
.设运动时间为![]()
![]() ,解答下列问题:
,解答下列问题:
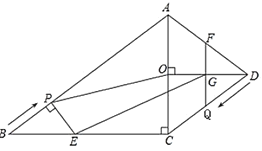
(1)当![]() 为何值时,点
为何值时,点![]() 在
在![]() 的平分线上?
的平分线上?
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 与
与![]() 的函数关系式.
的函数关系式.
(3)连接![]() ,
,![]() ,在运动过程中,是否存在某一时刻
,在运动过程中,是否存在某一时刻![]() ,使
,使![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3(a≠0)经过A(3,0),B(4,1)两点,且与y轴交于点C.
(1)求抛物线y=ax2+bx+3(a≠0)的函数关系式及点C的坐标;
(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求点E的坐标.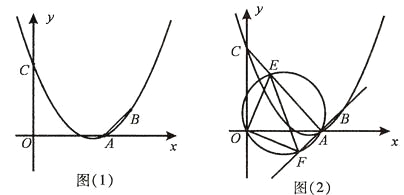
查看答案和解析>>
科目:初中数学 来源: 题型:
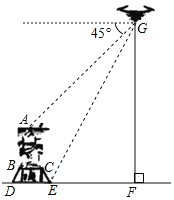
【题目】为了测量重庆有名的观景点南山大金鹰的大致高度,小南同学使用的无人机进行观察,当无人机与大金鹰侧面在同一平面,且距离水平面垂直高度GF为100米时,小南调整摄像头方向,当俯角为45°时,恰好可以拍摄到金鹰的头顶A点;当俯角为63°时,恰好可以拍摄到金鹰底座点E.已知大金鹰是雄踞在一人造石台上,石台侧面CE长12.5米,坡度为1:0.75,石台上方BC长10米,头部A点位于BC中点正上方.则金鹰自身高度约( )米.(结果保留一位小数,sin63°≈0.89,cos63°≈0.45,tan63°≈1.96)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com