
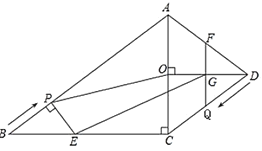
����Ŀ����֪����ͼ�����ı���![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��ֱƽ��
��ֱƽ��![]()
![]() .��
.��![]() �ӵ�
�ӵ�![]() ��������
��������![]() ���������˶����ٶ�Ϊ
���������˶����ٶ�Ϊ![]() ��ͬʱ����
��ͬʱ����![]() �ӵ�
�ӵ�![]() ��������
��������![]() ���������˶����ٶ�Ϊ
���������˶����ٶ�Ϊ![]() ����һ����ֹͣ�˶�����һ����Ҳֹͣ�˶�.����
����һ����ֹͣ�˶�����һ����Ҳֹͣ�˶�.����![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ������
������![]() ��
��![]() ���ֱ�
���ֱ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��![]() .����
.����![]() ��
��![]() .���˶�ʱ��Ϊ
.���˶�ʱ��Ϊ![]()
![]() ������������⣺
������������⣺
(1)��![]() Ϊ��ֵʱ����
Ϊ��ֵʱ����![]() ��
��![]() ��ƽ�����ϣ�
��ƽ�����ϣ�
(2)���ı���![]() �����Ϊ
�����Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵʽ.
�ĺ�����ϵʽ.
(3)����![]() ��
��![]() �����˶������У��Ƿ����ijһʱ��
�����˶������У��Ƿ����ijһʱ��![]() ��ʹ
��ʹ![]() �������ڣ����
�������ڣ����![]() ��ֵ���������ڣ���˵������.
��ֵ���������ڣ���˵������.
���𰸡�(1)![]() Ϊ4��ʱ����
Ϊ4��ʱ����![]() ��
��![]() ��ƽ�����ϣ�(2)S
��ƽ�����ϣ�(2)S![]()
![]() ��(3)��
��(3)��![]() ��ʱ��
��ʱ��![]() .
.
��������
��1�����ݹ��ɶ�����AC������![]() ֤
֤![]() �����CD��OD��ֵ��������BPE�ס�BAC�õ�����ʽ���ú���t�Ĵ���ʽ��ʾ��PE��BE������E�ڡ�BAC��ƽ������ʱ����ΪEP��AB��EC��AC���ɵ�PE=EC���ɴ˹������̼��ɽ�����⣮
�����CD��OD��ֵ��������BPE�ס�BAC�õ�����ʽ���ú���t�Ĵ���ʽ��ʾ��PE��BE������E�ڡ�BAC��ƽ������ʱ����ΪEP��AB��EC��AC���ɵ�PE=EC���ɴ˹������̼��ɽ�����⣮
��2������S�ı���OPEG=S��OEG+S��OPE=S��OEG+��S��OPC+S��PCE-S��OEC������������ϵʽ���ɣ�
��3��֤����EOC=��QOG���ɵ�tan��EOC=tan��QOG���Ƴ�![]() ���ɴ˹������̼��ɽ�����⣮
���ɴ˹������̼��ɽ�����⣮
(1)��![]() ����
����![]() ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��ֱƽ���߶�
��ֱƽ���߶�![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��![]() ��
��
��![]() ��
��![]() ��
��
���BPE=��BCA=90��
�֡�B=��B
���BPE�ס�BAC
��![]()
��![]()
��![]() ��
��![]() ��
��
����![]() ��
��![]() ��ƽ������ʱ��
��ƽ������ʱ��
��![]() ��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() .
.
�൱![]() Ϊ4��ʱ����
Ϊ4��ʱ����![]() ��
��![]() ��ƽ������.
��ƽ������.
(2)��ͼ������![]() ��
��![]() .
.
![]()
![]()
![]()
![]() .
.
(3)����.��ͼ������![]() .
.
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
��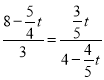 ��
��
�����ã�![]() ��
��
���![]() ��10(��)
��10(��)
�൱![]() ��ʱ��
��ʱ��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
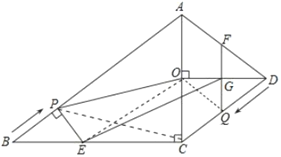
����Ŀ��������y��![]() x2��3mx+2m+1��x�������ύ��A��B���㣨A��B����ࣩ����y�������ύ�ڵ�C����OA��OC��
x2��3mx+2m+1��x�������ύ��A��B���㣨A��B����ࣩ����y�������ύ�ڵ�C����OA��OC��
��1�������ߵĽ���ʽΪ�� ����ֱ��д���������
��2����ͼ1��DΪy����һ�㣬����D��ֱ��y��![]() x+n����������E��F����EF��5
x+n����������E��F����EF��5![]() �����D�����ꣻ
�����D�����ꣻ
��3������AOC��ƽ����ij����ʱ����ת90������A'O'C'����A��C��O�Ķ�Ӧ��ֱ�ΪA'��C'��O'��������ת��ġ�A'O'C'ǡ����һ�ߵ������˵������������ϣ��������A'�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
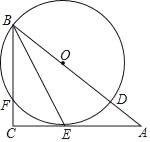
����Ŀ����Rt��ABC�У���ACB��90�㣬BEƽ�֡�ABC��D�DZ�AB��һ�㣬��BDΪֱ������O������E���ҽ�BC�ڵ�F
(1)��֤��AC����O�����ߣ�
(2)��CF��2��CE��4������O�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����ϵ���״�����������ABC,��BC=120mm,��4D=80mm, .�����ӹ��������������ͼ1,ʹ�����ε�һ����BC��,������������ֱ���AB,AC��.
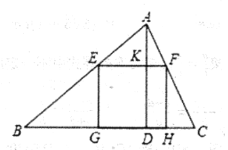
(1)��֤��![]() ;
;
(2)���������������ı߳�;
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() ��һԪ���η���
��һԪ���η���![]() .
.
��1����֤��������������ʵ������
��2����������һ��С��1����![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����С�����ι��ɵ������У�ÿ��С�����εĶ���������.
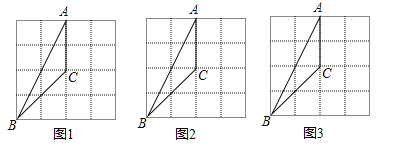
��1��![]() ���������㶼�ڸ����.
���������㶼�ڸ����.
����ͼ1�У�����һ����![]() �����ĶԳƵĸ�������Σ�
�����ĶԳƵĸ�������Σ�
����ͼ2�У�����һ����![]() ����Գ�����
����Գ�����![]() �й����ߵĸ�������Σ�
�й����ߵĸ�������Σ�
����ͼ3�У�����![]() ���ŵ�
���ŵ�![]() ��˳ʱ�뷽����ת
��˳ʱ�뷽����ת![]() ���������.
���������.
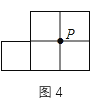
��2����ͼ4����5���߳�Ϊ1��С������ƴ�ɵ�ͼ�Σ���ѡ���ʵ��ĸ�㣬���̶ȵ�ֱ���澭����![]() ��һ��ֱ�ߣ�ʹ��ƽ�ָ�ͼ�ε�������������ߵĺۼ�����Ҫ��˵������.
��һ��ֱ�ߣ�ʹ��ƽ�ָ�ͼ�ε�������������ߵĺۼ�����Ҫ��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
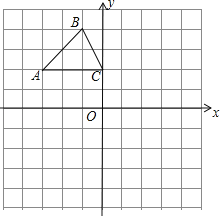
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���֪��ABC�������������ֱ���A(��3��2)��B(��1��4)��C(0��2)��
(1)�뻭����ABC���ڵ�O�ĶԳ�ͼ�Ρ�A1B1C1��
(2)����ABC��ԭ��O��ʱ����ת90���õ���A2B2C2���뻭����A2B2C2���������ת�����е�B��������Բ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
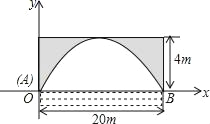
����Ŀ����һ���������ι��ţ�����ˮλʱ����ˮ���Ϊ20m��������ˮ��4m��
��1������ͼ��ֱ������ϵ�У�����������ߵĽ���ʽ��
��2��Ϊ��֤������ֻ˳�����У�����ˮ����Ȳ���С��18m����ˮ��������ˮλ�����ϣ�����Ƕ����ף�����Ӱ�������ֻ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ��ͼ��x����A����2��0���͵�B����y�Ḻ�����ڵ�C����OB=OC�����н��ۣ�
��ͼ��x����A����2��0���͵�B����y�Ḻ�����ڵ�C����OB=OC�����н��ۣ�
��2b��c=2����a=![]() ����ac=b��1����
����ac=b��1����![]() ��0
��0
������ȷ�ĸ����У�������

A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com