
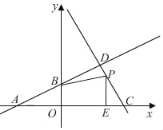
【题目】如图,在平面直角坐标系中,直线y=![]() x+2与x轴、y轴的交点分别为A、B,直线y=﹣2x+12交x轴于C,两条直线的交点为D;点P是线段DC上的一个动点,过点P作PE⊥x轴,交x轴于点E,连接BP;
x+2与x轴、y轴的交点分别为A、B,直线y=﹣2x+12交x轴于C,两条直线的交点为D;点P是线段DC上的一个动点,过点P作PE⊥x轴,交x轴于点E,连接BP;
(1)求△DAC的面积;
(2)在线段DC上是否存在一点P,使四边形BOEP为矩形;若存在,写出P点坐标;若不存在,说明理由;
(3)若四边形BOEP的面积为S,设P点的坐标为(x,y),求出S关于x的函数关系式,并写出自变量x的取值范围.
【答案】(1)S△DAC=20;(2)存在, 点P的坐标是(5,2);(3)S=﹣x2+7x(4≤x<6).
【解析】
(1)想办法求出A、D、C三点坐标即可解决问题;
(2)存在.根据OB=PE=2,利用待定系数法即可解决问题;
(3)利用梯形的面积公式计算即可;
(1)当y=0时,![]() x+2=0,
x+2=0,
∴x=﹣4,点A坐标为(﹣4,0)
当y=0时,﹣2x+12=0,
∴x=6,点C坐标为(6,0)
由题意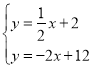 ,解得
,解得![]() ,
,
∴点D坐标为(4,4)
∴S△DAC=![]() ×10×4=20.
×10×4=20.
(2)存在,∵四边形BOEP为矩形,
∴BO=PE
当x=0时,y=2,点B坐标为(0,2),
把y=2代入y=﹣2x+12得到x=5,
点P的坐标是(5,2).
(3)∵S=![]() (OB+PE)OE
(OB+PE)OE
∴S=![]() (2﹣2x+12)x=﹣x2+7x(4≤x<6).
(2﹣2x+12)x=﹣x2+7x(4≤x<6).


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】小明和小亮计划暑期结伴参加志愿者活动.小明想参加敬老服务活动,小亮想参加文明礼仪宣传活动.他们想通过做游戏来决定参加哪个活动,于是小明设计了一个游戏,游戏规则是:在三张完全相同的卡片上分别标记4、5、6三个数字,一人先从三张卡片中随机抽出一张,记下数字后放回,另一人再从中随机抽出一张,记下数字,若抽出的两张卡片标记的数字之和为偶数,则按照小明的想法参加敬老服务活动,若抽出的两张卡片标记的数字之和为奇数,则按照小亮的想法参加文明礼仪宣传活动.你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
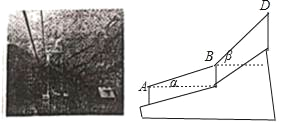
【题目】如图,小明到青城山游玩,乘坐缆车,当登山缆车的吊箱经过点A到达点B时,它经过了200 m,缆车行驶的路线与水平夹角∠α=16°,当缆车继续由点B到达点D时,它又走过了200 m,缆车由点B到点D的行驶路线与水平夹角∠β=42°,求缆车从点A到点D垂直上升的距离.(结果保留整数)(参考数据:sin16°≈0.27,cos16°≈0.77,sin42°≈0.66,cos42°≈0.74)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A(―3,6)、B(―9,一3),以原点O为位似中心,相似比为![]() ,把△ABO缩小,则点A的对应点A′的坐标是( )
,把△ABO缩小,则点A的对应点A′的坐标是( )

A.(―1,2)
B.(―9,18)
C.(―9,18)或(9,―18)
D.(―1,2)或(1,―2)
查看答案和解析>>
科目:初中数学 来源: 题型:
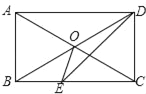
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC=90°,对角线AC,BD交于点O,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
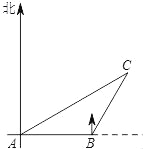
【题目】如图,一艘渔船正自西向东航行追赶鱼群,在A处望见岛C在船的北偏东60°方向,前进20海里到达B处,此时望见岛C在船的北偏东30°方向,以岛C为中心的12海里内为军事演习的危险区.请通过计算说明:如果这艘渔船继续向东追赶鱼群是否有进入危险区的可能.(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发型了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQO使得∠O=90°,点Q在在直角坐标系y轴正半轴上,点P在x轴正半轴上,点O与原点重合,∠OQP=60°,点H在边QO上,点D、E在边PO上,点G、F在边PQ上,那么点P坐标为___________.
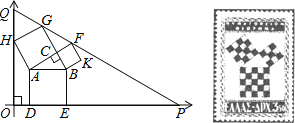
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)我市开展了“寻找雷锋足迹”的活动,某中学为了了解七年级800名学生在“学雷锋活动月”中做好事的情况,随机调查了七年级50名学生在一个月内做好事的次数,并将所得数据绘制成统计图,请根据图中提供的信息解答下列问题:
①所调查的七年级50名学生在这个月内做好事次数的平均数是 ,众数是 ,极差是 :
②根据样本数据,估计该校七年级800名学生在“学雷锋活动月”中做好事不少于4次的人数.
(2)甲口袋有2个相同的小球,它们分别写有数字1和2;乙口袋中装有3个相同的小球,它们分别写有数字3、4和5,从这两个口袋中各随机地取出1个小球.
①用“树状图法”或“列表法”表示所有可能出现的结果;
②取出的两个小球上所写数字之和是偶数的概率是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com