
����Ŀ����ͼ����֪���κ���![]() cΪ����
cΪ����![]() ��ͼ����
��ͼ����![]() ����
����![]() ��������M������A��
������Ϊ��M������A��![]() �ᣬ��y���ڵ�D�����ö��κ���ͼ���ڵ�B������BC��
�ᣬ��y���ڵ�D�����ö��κ���ͼ���ڵ�B������BC��
![]() ��ö��κ����Ľ���ʽ����M�����꣮
��ö��κ����Ľ���ʽ����M�����꣮
![]() ���ö��κ���ͼ����һ��P��y���ƽ���ߣ���
���ö��κ���ͼ����һ��P��y���ƽ���ߣ���![]() һ���ڵ�Q���Ƿ���ڵ�P��ʹ���Ե�P��Q��C��OΪ������ı���Ϊƽ���ı��Σ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�
һ���ڵ�Q���Ƿ���ڵ�P��ʹ���Ե�P��Q��C��OΪ������ı���Ϊƽ���ı��Σ������ڣ����P�����ꣻ�������ڣ�˵�����ɣ�
![]() ��N������CA�ϵĶ��㣬����M��C��N�����ɵ���������
��N������CA�ϵĶ��㣬����M��C��N�����ɵ���������![]() ���ƣ���ֱ��д�����е�N������
���ƣ���ֱ��д�����е�N������![]() ֱ��д�����������д������
ֱ��д�����������д������![]() ��
��

���𰸡�![]() ���κ�������ʽΪ
���κ�������ʽΪ![]() ����M������Ϊ
����M������Ϊ![]() ��
��![]() ����ƽ���ı��Σ�
����ƽ���ı��Σ�![]() ��
��![]()
![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��������
![]() ����A����C��������뺯������ʽ���������b��c��ֵ��ͨ���䷽���õ���M�����ꣻ
����A����C��������뺯������ʽ���������b��c��ֵ��ͨ���䷽���õ���M�����ꣻ
![]() ����ƽ���ı��ε��ж��Ա�ƽ������ȣ��ɵù���m�ķ��̣����ݽⷽ�̣��ɵô𰸣�
����ƽ���ı��ε��ж��Ա�ƽ������ȣ��ɵù���m�ķ��̣����ݽⷽ�̣��ɵô𰸣�
![]() ����������ɵ�
����������ɵ�![]() ������
������![]() ��
��![]() ���ƣ���Ҫ���з������ۣ��ֳ�
���ƣ���Ҫ���з������ۣ��ֳ�![]() ��
��![]() ��
��![]() ��
��![]() ���֣�Ȼ�����ñߵĶ�Ӧ��ֵ���N������ĺ����꣬�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵô𰸣�
���֣�Ȼ�����ñߵĶ�Ӧ��ֵ���N������ĺ����꣬�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵô𰸣�
![]() �ѵ�
�ѵ�![]() ����
����![]() ��������
������κ���![]() �ã�
�ã�
![]() ���
���![]()
![]() ���κ�������ʽΪ
���κ�������ʽΪ![]() ��
��
�䷽��![]() ��
��
![]() ��M������Ϊ
��M������Ϊ![]() ��
��
![]() ��
��![]() ֪����
֪����![]() ʱ��
ʱ��
![]() ��
��
��֮��![]() ��
��![]()
![]()
![]() ��
��![]()
��P�������Ϊm��
![]() ��PQ��BC���ཻʱ��
��PQ��BC���ཻʱ��
![]() ��
��
![]() ��ʱ������ƽ���ı��Σ�
��ʱ������ƽ���ı��Σ�
![]() ��PQ��AC���ཻʱ��
��PQ��AC���ཻʱ��
��![]() ��
��![]() �ɵ�ֱ��AC����ʽ
�ɵ�ֱ��AC����ʽ
![]() ��
��
![]() ��
��![]()
![]() ��
��
��![]()
![]() ��
��
![]() ��
��
![]() ��
��
�˷����⣬
![]() ��ʱ������ƽ���ı��Σ�
��ʱ������ƽ���ı��Σ�
![]() ��PQ��AB���ཻʱ��
��PQ��AB���ཻʱ��
![]() ��
��![]()
![]() ��
��
��![]()
![]() ��
��
����![]() ��
��
���![]() ��
��
��![]() ʱ��
ʱ��![]() ��
��
![]() ������Ϊ
������Ϊ![]() ��
��
��ʱ������ƽ���ı��Σ�![]() ��
��
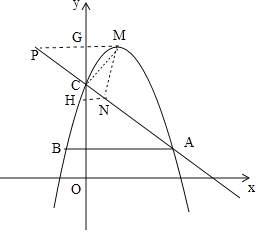
![]() ����MC����
����MC����![]() �Ტ�ӳ���AC�ڵ�N�����G����Ϊ
�Ტ�ӳ���AC�ڵ�N�����G����Ϊ![]()
 ��
��
![]() ��
��![]()
![]() ��
��
��![]() ����
����![]() ���
���![]() �����P����Ϊ
�����P����Ϊ![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
�ɴ˿�֪������N��AC�ϣ���![]() �����D���C��Ϊ���������ζ�Ӧ��
�����D���C��Ϊ���������ζ�Ӧ��
![]() ����
����![]() ��
��![]() ������
������![]() ��
��
![]() ��
��![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
����N��y���Ҳ࣬��![]() �ᣬ
�ᣬ
![]() ��
��![]()
![]() ��
��
��![]() ����
����![]() �����
�����![]() ��
��
![]() ��
��
ͬ���ɵã�����N��y����࣬
��![]() ����
����![]() �����
�����![]()
![]() ��
��
![]() ����
����![]() ��
��![]() ������
������![]()
![]() ��
��
![]() ��
��
����N��y���Ҳ࣬��![]() ����
����![]() �����
�����![]() ��
��
����N��y����࣬��![]() ����
����![]() �����
�����![]()
![]() ��
��![]() ��
��
![]() ���з�������õ�N������4�����ֱ�Ϊ
���з�������õ�N������4�����ֱ�Ϊ![]() ��
��![]() ��
��![]() ��
��![]() ��
��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������е���ʦ������æ������һ�꼶�ܶ���ѧ��ʦ��Ȼ��ֶ������壬��������ʦ�;�����ַ�����һ�ߣ�ij������������ѧУ���������������빫���ڹ�����Ϣ��һ�����ѧУ���£��첽�ϻ�ѧУ�������ܷ�ӳ��������ʦ��ѧУ�ľ���y��ʱ��x�Ĺ�ϵ�Ĵ���ͼ���ǣ�������
A. B.
B.
C. D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(1)�۲����
��ͼ��,��B��A��C��ͬһ��ֱ����,DB��BC,EC��BC����DAE=90�㣬AD=AE,��BC��BD��CE֮���������ϵΪ

(2)������
��ͼ��,��Rt��ABC��,��ABC=90����CB=8��AB=4����ACΪֱ�DZ�����������Rt��DAC����BD,��BD�ij���
(3)��չ����
��ͼ��,���ı���ABCD��,��ABC=��ADC=90����CB=8.AB=4��DC=DA����BD=
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����AOB��25������M��N�ֱ��DZ�OA��OB�ϵĶ��㣬��P��Q�ֱ��DZ�OB��OA�ϵĶ��㣬�ǡ�MPQ��������PQN��������MP��PQ��QN��Сʱ������������ֵΪ��������
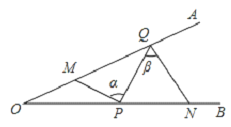
A.50��B.40��C.30��D.25��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
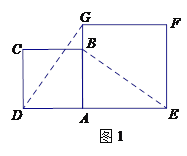
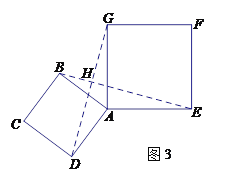
����Ŀ������������12�֣�����ѧ��ȤС���У�С��������ѧ̽��������߳�Ϊ2��������ABCD��߳�Ϊ![]() ��������AEFG��ͼ1λ�÷��ã�AD��AE��ͬһ��ֱ���ϣ�AB��AG��ͬһ��ֱ���ϣ�
��������AEFG��ͼ1λ�÷��ã�AD��AE��ͬһ��ֱ���ϣ�AB��AG��ͬһ��ֱ���ϣ�
��1��С������![]() ���������˵�����ɣ�
���������˵�����ɣ�
��2����ͼ2��С����������ABCD�Ƶ�A��ʱ����ת������Bǡ�������߶�DG��ʱ��������������ʱBE�ij���
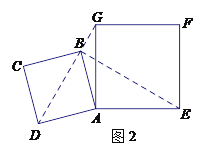
��3����ͼ3����С����������ABCD�Ƶ�A������ʱ����ת���߶�DG���߶�BE���ཻ������ΪH��д����![]() ����
����![]() ���֮�͵����ֵ������Ҫ˵�����ɣ�
���֮�͵����ֵ������Ҫ˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֤�����̲���������
��ͼ��DE��AB��FG��AC����1=��3����֤��BD��AC��
֤������DE��AB(��֪)��
���1=_______(_______)
�ߡ�1=��3(��֪)��
���3=_______(��������)��
��FG��BD(_______)��
���ADB=��AFG(_______)
��FG��AC(��֪)��
���AFG=90��(��ֱ�Ķ���)��
���ADB=90��(_______)��
��BD��AC(_______)

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ��ҵ����硱��ڼ䣬������ָ�����õ�����ũ�������ɵõ�����Ʒ�ۼ�13%�IJ�������������С�����һ̨A��ϴ�»���С��������һ̨B��ϴ�»�����һ���õ���������351Ԫ����֪B��ϴ�»��ۼ۱�A��ϴ�»��ۼ۶�500Ԫ����
��1��A��ϴ�»���B��ϴ�»����ۼ۸��Ƕ���Ԫ?
��2��С���С������ϴ�»�������������ʵ�ʸ��������Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����MON=30������A1��A2��A3������ON�ϣ���B1��B2��B3��������OM�ϣ���A1B1A2����A2B2A3����A3B3A4����Ϊ�ȱ������Σ���OA1=a������A7B7A8�ı߳�Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����DCE=90����CD=CE��AD��AC��BE��AC������ֱ�ΪA��B��

��֤���١�ADC�ա�BCE��
��AD+AB=BE��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com