
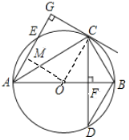
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为F,CG⊥AE,交弦AE的延长线于点G,且CG=CF.
(1)求证:CG是⊙O的切线;
(2)若AE=2,EG=1,求由弦BC和![]() 所围成的弓形的面积.
所围成的弓形的面积.

【答案】(1)见解析;(2)![]()
【解析】
(1)连接OC得∠ACO=∠BAC,证明Rt△ACG≌Rt△ACF得∠CAG=∠CAB,所以∠ACO=∠CAG,故OC∥AG,可证明∠OCG+∠G=180°,进而可得结论;
(2) 过点O作OM⊥AE,得AM=ME=1,再证明四边形OCGM为矩形得OC=2,从而可求得OF=1,进而得∠COF=60°,再根据S弓形BC=S扇形OBC- S△OBC求解即可.
(1)证明:连接OC.
∴OA=OC
∴∠ACO=∠BAC
∵CD⊥AB,CG⊥AE,
∴∠CGA=∠CFA=90°
∵CG=CF,AC=AC
∴Rt△ACG≌Rt△ACF
∴∠CAG=∠CAB,
∴∠ACO=∠CAG
∴OC∥AG,
∴∠OCG+∠G=180°
∵∠CGA=90°
∴∠OCG=90°,即![]() ,
,
∴CG是⊙O的切线.
(2)过点O作OM⊥AE,垂足为M,
则AM=ME=![]() AE=1,∠OMG=∠OCG=∠G=90°.
AE=1,∠OMG=∠OCG=∠G=90°.
∴四边形OCGM为矩形,
∴OC=MG=ME+EG=2.
在Rt△AGC和Rt△AFC中
![]()
∴Rt△AGC≌Rt△AFC,
∴AF=AG=AE+EG=3,
∴OF=AF-OA=1,
在Rt△COF中,
∵cos∠COF=![]() =
=![]() .
.
∴∠COF=60°,CF=OC·sin∠COF=2×![]() =
=![]() ,
,
∴S弓形BC=![]() -
-![]() ×2×
×2×![]() =
=![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,AB=2,且∠ABC=∠ABE=60°,M为对角线BD(不含B点)上任意一点,将BM绕点B逆时针旋转60°得到BN,连接EN、AM、CM,则AM+BM+CM的最小值为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
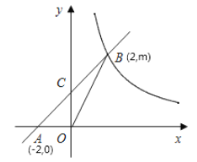
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与反比例函数第一象限内的图象交于点
,与反比例函数第一象限内的图象交于点![]() ,连接
,连接![]() ,若
,若![]() .
.
(1)求直线![]() 的表达式和反比例函数的表达式;
的表达式和反比例函数的表达式;
(2)若直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“30元”的字样.规定:顾客在本商场同一日内,每消费满200元,就可以在箱子里先后摸出两个球(第一次摸出后不放回),商场根据两小球所标金额的和返还相应价格的购物券,可以重新在本商场消费,某顾客刚好消费200元.
(1)该顾客至少可得到_____元购物券,至多可得到_______元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于30元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AD=5,点E、F是正方形ABCD内的两点,且AE=FC=3,BE=DF=4,则EF的长为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着经济的快速发展,环境问题越来越受到人们的关注.某校学生会为了了解垃圾分类知识的普及情况,随机调查了部分学生,调查结果分为“非常了解”“了解”“了解较少”“不了解”四类,并将调查结果绘制成下面两幅统计图.

(1)求:本次被调查的学生有多少名?补全条形统计图.
(2)估计该校1200名学生中“非常了解”与“了解”的人数和是多少.
(3)被调查的“非常了解”的学生中有2名男生,其余为女生,从中随机抽取2人在全校做垃圾分类知识交流,请利用画树状图或列表的方法,求恰好抽到一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣4).
的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴相交于点C(0,﹣4).
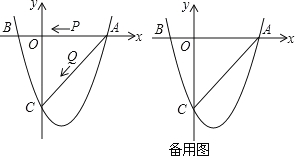
(1)求该二次函数的解析;
(2)若点P、Q同时从A点出发,以每秒1个单位长度的速度分别沿AB、AC边运动,其中一点到达端点时,另一点也随之停止运动.
①当点P运动到B点时,在x轴上是否存在点E,使得以A、E、Q为顶点的三角形为等腰三角形?若存在,请求出E点的坐标;若不存在,请说明理由.
②当P、Q运动到t秒时,△APQ沿PQ翻折,点A恰好落在抛物线上D点处,请直接写出t的值及D点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
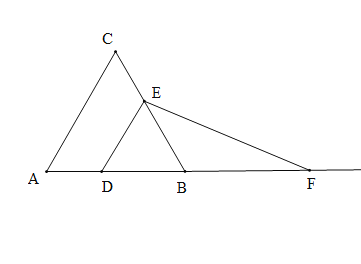
【题目】如图,已知![]() 为等边三角形,
为等边三角形,![]() ,点
,点![]() 为边
为边![]() 上一点,过点
上一点,过点![]() 作
作![]() .交
.交![]() 于
于![]() 点;过
点;过![]() 点作
点作![]() ,交
,交![]() 的延长线于
的延长线于![]() 点.设
点.设![]() ,
,![]() 的面积为
的面积为![]() ,则能大致反映
,则能大致反映![]() 与
与![]() 函数关系的图象是( )
函数关系的图象是( )
A.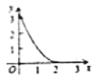 B.
B.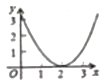
C.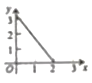 D.
D.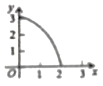
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年疫情期间,为了更好地落实“停课不停学”行动,我市某中学为了更好督促学生学习,组织教师对某班学生进行家访,根据学生参加网络学习效果划分为![]() (差),
(差),![]() (中),
(中),![]() (优),
(优),![]() (良)四个等级,并绘制了下面不完整的统计图表,根据图表中提供的信息解答下列问题;
(良)四个等级,并绘制了下面不完整的统计图表,根据图表中提供的信息解答下列问题;
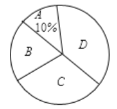
(1)求![]() ,
,![]() 的值;
的值;
(2)求![]() 等级对应扇形圆心角的度数;
等级对应扇形圆心角的度数;
(3)学校要从![]() 等级的学生中随机选取2人参加李老师个性化辅导,用列表或画树状图求
等级的学生中随机选取2人参加李老师个性化辅导,用列表或画树状图求![]() 等级中的学生小慧被选中参加辅导的概率.
等级中的学生小慧被选中参加辅导的概率.
效果等级 | 频数 | 频率 |
| 5 | |
| ||
|
| 0.3 |
| 20 |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com