
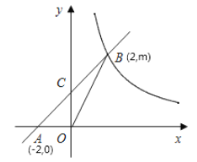
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与反比例函数第一象限内的图象交于点
,与反比例函数第一象限内的图象交于点![]() ,连接
,连接![]() ,若
,若![]() .
.
(1)求直线![]() 的表达式和反比例函数的表达式;
的表达式和反比例函数的表达式;
(2)若直线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,求
,求![]() 的面积.
的面积.
【答案】(1)![]() ,
,![]() ;(2)2
;(2)2
【解析】
(1)先由S△AOB=4,求得点B的坐标是(2,4),把点B(2,4)代入反比例函数的解析式为![]() ,可得反比例函数的解析式为:
,可得反比例函数的解析式为:![]() ;再把A(-2,0)、B(2,4)代入直线AB的解析式为y=ax+b可得直线AB的解析式为y=x+2.
;再把A(-2,0)、B(2,4)代入直线AB的解析式为y=ax+b可得直线AB的解析式为y=x+2.
(2)把x=0代入直线AB的解析式y=x+2得y=2,即OC=2,可得S△OCB=![]() OC×2=
OC×2=![]() ×2×2=2.
×2×2=2.
解:(1)由A(-2,0),得OA=2;
∵点B(2,m)在第一象限内,S△AOB=4,
∴![]() OAm=4;
OAm=4;
∴m=4;
∴点B的坐标是(2,4);
设该反比例函数的解析式为![]() (k≠0),
(k≠0),
将点B的坐标代入,得![]() ,
,
∴k=8;
∴反比例函数的解析式为:![]() ;
;
设直线AB的解析式为y=ax+b(k≠0),
将点A,B的坐标分别代入,得
![]() ,
,
解得:![]() ;
;
∴直线![]() 的表达式是
的表达式是![]() ;
;
(2)在y=x+2中,令x=0,得y=2.
∴点C的坐标是(0,2),
∴OC=2;
∴S△OCB=![]() OC×2=
OC×2=![]() ×2×2=2.
×2×2=2.


科目:初中数学 来源: 题型:
【题目】随着智能手机的普及率越来越高以及移动支付的快捷高效性,中国移动支付在世界处于领先水平.为了解人们平时最喜欢用哪种移动支付方式,因此在某步行街对行人进行随机抽样调查,以下是根据调查结果分别整理的不完整的统计表和统计图.
移动支付方式 | 支付宝 | 微信 | 其他 |
人数/人 |
| 200 | 75 |
请你根据上述统计表和统计图提供的信息.完成下列问题:
(1)在此次调查中,使用支付宝支付的人数;
(2)求表示微信支付的扇形所对的圆心角度数;
(3)某天该步行街人流量为10万人,其中30%的人购物并选择移动支付,请你依据此次调查获得的信息估计一下当天使用微信支付的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设![]() 都是实数,且
都是实数,且![]() .我们规定:满足不等式
.我们规定:满足不等式![]() 的实数
的实数![]() 的所有值的全体叫做闭区间、表示为
的所有值的全体叫做闭区间、表示为![]() .对于一个函数,如果它的自变量
.对于一个函数,如果它的自变量![]() 与函数值
与函数值![]() 满足:当
满足:当![]() 时,有
时,有![]() ,我们就称此函数是闭区间
,我们就称此函数是闭区间![]() 上的“闭函数”.
上的“闭函数”.
(1)反比例函数![]() 是闭区间
是闭区间![]() 上的“闭函数”吗?请判断并说明理由;
上的“闭函数”吗?请判断并说明理由;
(2)若一次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”,求此一次函数的解析式;
上的“闭函数”,求此一次函数的解析式;
(3)若实数![]() 满足
满足![]() .且
.且![]() ,当二次函数
,当二次函数![]() 是闭区间
是闭区间![]() 上的“闭函数”时,求
上的“闭函数”时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
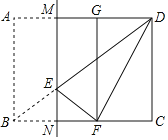
【题目】如图,在矩形ABCD中,AB:BC=3:4,点E是对角线BD上一动点(不与点B,D重合),将矩形沿过点E的直线MN折叠,使得点A,B的对应点G,F分别在直线AD与BC上,当△DEF为直角三角形时,CN:BN的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
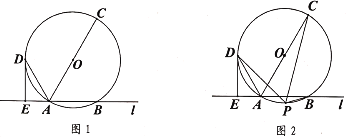
【题目】如图1,直线![]() 与
与![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() 是
是![]() 的直径,
的直径,![]() 是
是![]() 上一点,
上一点,![]() 于点
于点![]() ,连结
,连结![]() ,且
,且![]() 平分
平分![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的半径;
的半径;
(3)如图2,在(2)的条件下,点![]() 为
为![]() 上一动点,连接
上一动点,连接![]() ,
,![]() ,
,![]() ,问:线段
,问:线段![]() ,
,![]() ,
,![]() 之间存在什么数量关系?请说明理由.
之间存在什么数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
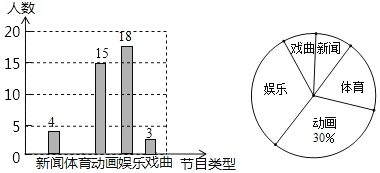
【题目】某学校为了解全校学生对电视节目的喜爱情况(新闻、体育、动画、娱乐、戏曲),从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.
请根据以上信息,解答下列问题:
(1)这次被调查的学生共有多少人?并将条形统计图补充完整;
(2)在扇形统计图中,“体育”对应的圆心角的度数是?
(3)若该校约有1500名学生,估计全校学生中喜欢娱乐节目的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,弦CD⊥AB,垂足为F,CG⊥AE,交弦AE的延长线于点G,且CG=CF.
(1)求证:CG是⊙O的切线;
(2)若AE=2,EG=1,求由弦BC和![]() 所围成的弓形的面积.
所围成的弓形的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com