
【题目】如图,在大楼AB的正前方有一斜坡CD,CD=4米,坡角∠DCE=30°,小红在斜坡下的点C处测得楼顶B的仰角为60°,在斜坡上的点D处测得楼顶B的仰角为45°,其中点A、C、E在同一直线上.
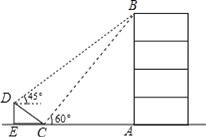
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度(结果保留根号)
【答案】(1)2米;(2)(6+![]() )或(6-
)或(6-![]() )米.
)米.
【解析】试题分析:(1)在在Rt△DCE中,利用30°所对直角边等于斜边的一半,可求出DE=2米;(2)过点D作DF⊥AB于点F,则AF=2,根据三角函数可用BF表示BC、BD,然后可判断△BCD是Rt△,进而利用勾股定理可求得BF的长,AB的高度也可求.
试题解析:(1)在Rt△DCE中,∠DEC=90°,∠DCE=30°,∴DE=![]() DC=2米;(2)过D作DF⊥AB,交AB于点F,则AF=DE=2米.∵∠BFD=90°,∠BDF=45°,∴∠BFD=45°,∴BF=DF.设BF=DF=x米,则AB=(x+2)米,在Rt△ABC中,∠BAC=90°,∠BCA=60°,∴sin∠BCA=
DC=2米;(2)过D作DF⊥AB,交AB于点F,则AF=DE=2米.∵∠BFD=90°,∠BDF=45°,∴∠BFD=45°,∴BF=DF.设BF=DF=x米,则AB=(x+2)米,在Rt△ABC中,∠BAC=90°,∠BCA=60°,∴sin∠BCA=![]() ,∴BC=AB÷sin∠BCA=(x+2)÷
,∴BC=AB÷sin∠BCA=(x+2)÷![]() =
=![]() 米,在Rt△BDF中,∠BFD=90°,
米,在Rt△BDF中,∠BFD=90°,![]() 米,∵∠DCE=30°,∠ACB=60°,∴∠DCB=90°.∴
米,∵∠DCE=30°,∠ACB=60°,∴∠DCB=90°.∴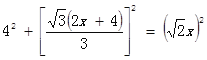 ,解得:x=4+
,解得:x=4+![]() 或x=4﹣
或x=4﹣![]() ,则AB=(6+
,则AB=(6+![]() )米或(6﹣
)米或(6﹣![]() )米.
)米.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,∠A,∠B,∠C,∠D度数之比为1:2:3:3,则∠B的度数为( )
A. 30° B. 40° C. 80° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(﹣10)+(+7)
(2)12﹣(﹣18)+(﹣7)﹣15
(3)5.6+(﹣0. 9)+4.4+(﹣8.1)+(﹣0.1)
(4)|﹣22+(﹣3)2|﹣(﹣![]() )3
)3
(5)2×(﹣3)2﹣33﹣6÷(﹣2)
(6)﹣81÷![]() ×(﹣
×(﹣![]() )
)
(7)![]() +(﹣
+(﹣![]() )﹣(﹣
)﹣(﹣![]() )+(﹣
)+(﹣![]() )﹣(+
)﹣(+![]() )
)
(8)(﹣1)2008+(﹣5)×[(﹣2)3+2]﹣(﹣4)2÷(﹣![]() )
)
(9)﹣32×(﹣![]() )2+(
)2+(![]() ﹣
﹣![]() +
+![]() )×(﹣24).
)×(﹣24).
查看答案和解析>>
科目:初中数学 来源: 题型:
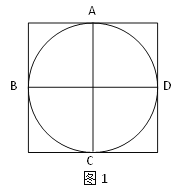
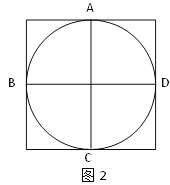
【题目】在图1、图2中,⊙O经过了正方形网格中的格点A、B、C、D,现请你仅用无刻度的直尺分别在图1、图2中画出一个满足下列条件的∠P:
(1)顶点P在⊙O上且不能与点A、B、C、D重合;
(2)∠P在图1、图2中的正切值分别为1、![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学科竞赛为参加区级比赛做选手选拔工作,经过多次测试后,有四位同学成为晋级的候选人,具体情况如下表:
甲 | 乙 | 丙 | 丁 | |
平均分 | 92 | 94 | 94 | 92 |
方 差 | 35 | 35 | 23 | 23 |
如果从这四位同学中选出一名晋级(总体水平高且状态稳定),童威会推荐( )
A. 甲 B. 乙 C. 丙 D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.

(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com