
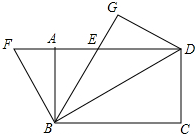
 ��ͼ������ABCD�У�AB=2$\sqrt{3}$��BC=6�����þ����ضԽ���BD���ۣ�ʹ��DBG���DBC��ͬһƽ���ڣ�C�Ķ�Ӧ��ΪG��BG��AD�ڵ�E����BEΪ�����ȱ�������PEF��P��B�غϣ�����E��Fλ��AB���࣬����PAF������BD����ƽ�ƣ���P�����Dʱֹͣƽ�ƣ���ƽ�ƽ���������P�����Dʱ��������PAF�Ƶ�P˳ʱ����תһ���ǶȦ���0������180�㣩��A�Ķ�Ӧ��A�䣬F�Ķ�Ӧ��F�䣬ֱ��PF����ֱ��BG�Ľ���ΪM��ֱ��F��A����ֱ��BG�Ľ���ΪN������ת�����У�����F��MN��ֱ�������Σ��ҡ�MNF��=90��ʱ����F��N�ij���Ϊ2$\sqrt{3}$-2��
��ͼ������ABCD�У�AB=2$\sqrt{3}$��BC=6�����þ����ضԽ���BD���ۣ�ʹ��DBG���DBC��ͬһƽ���ڣ�C�Ķ�Ӧ��ΪG��BG��AD�ڵ�E����BEΪ�����ȱ�������PEF��P��B�غϣ�����E��Fλ��AB���࣬����PAF������BD����ƽ�ƣ���P�����Dʱֹͣƽ�ƣ���ƽ�ƽ���������P�����Dʱ��������PAF�Ƶ�P˳ʱ����תһ���ǶȦ���0������180�㣩��A�Ķ�Ӧ��A�䣬F�Ķ�Ӧ��F�䣬ֱ��PF����ֱ��BG�Ľ���ΪM��ֱ��F��A����ֱ��BG�Ľ���ΪN������ת�����У�����F��MN��ֱ�������Σ��ҡ�MNF��=90��ʱ����F��N�ij���Ϊ2$\sqrt{3}$-2�� ���� ����������������Ǻ�����ϵ�Լ����ɶ����ó�BD��BE�ij����������DE�ij����ٽ��ƽ������ת�����ʡ�����������Ǻ�����ϵ�ֱ�����𰸣�
��� 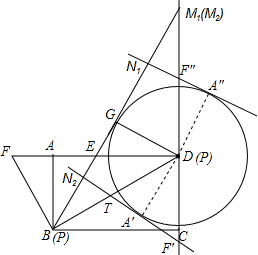 �⣺��ͼ���߾���ABCD�У�AB=2$\sqrt{3}$��BC=6��
�⣺��ͼ���߾���ABCD�У�AB=2$\sqrt{3}$��BC=6��
��tan��DBC=$\frac{2\sqrt{3}}{6}$=$\frac{\sqrt{3}}{3}$��
���DBC=30�㣬
���ABE=��ABF=��DBC=30�㣬
��AB=2$\sqrt{3}$��
��AF=AB��tan30��=2��
��FB=4��
��AD��BC��
���M1ED�ס�M1BC��
��$\frac{ED}{BC}$=$\frac{{M}_{1}D}{{M}_{1}C}$��
��$\frac{6-2}{6}$=$\frac{{M}_{1}D}{2\sqrt{3}+{M}_{1}D}$��
��ã�M1D=4$\sqrt{3}$��
��DF��=4��
��M1F��=4��$\sqrt{3}$-1����
��F��N1=$\frac{1}{2}$��4��$\sqrt{3}$-1��=2$\sqrt{3}$-2��
��AB=2$\sqrt{3}$��BC=6��
��BD=4$\sqrt{3}$��
��TD=BF=4��
��BT=4$\sqrt{3}$-4��
��TN2=$\frac{1}{2}$��4$\sqrt{3}$-4��=2$\sqrt{3}$-2��
�ߡ�ABD=��BDC=60�㣬��DTF��=60�㣬
���DTF���ǵȱ������Σ�
��DT=TF��=4��
��F��N2=4+2$\sqrt{3}$-2=2$\sqrt{3}$+2������ʱ��ת�Ǵ���180�㣬����������ȥ����
����������F��N=2$\sqrt{3}$-2��
�ʴ�Ϊ��2$\sqrt{3}$-2��
���� ������Ҫ�����˼��α任�ۺ��Լ�������Ǻ�����ϵ���ɶ�������ת�����ʵ�֪ʶ�����÷������۵ó��ǽ���ؼ���


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
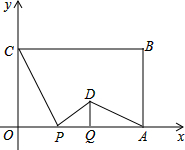 ��ͼ����ƽ��ֱ������ϵ�У�����OABC������OA��OC�ֱ���x�ᡢy����������ϣ�OA=8��OC=4����P�ӵ�O��������x����ÿ��2����λ�����ٶ����A�����˶�������P�����Aʱֹͣ�˶������P�˶���ʱ����t�룮���߶�CP���е��Ƶ�P��˳ʱ�뷽����ת90��õ�D����D���P���˶����˶�������DP��DA������D��DQ��OA����OA�ڵ�Q��
��ͼ����ƽ��ֱ������ϵ�У�����OABC������OA��OC�ֱ���x�ᡢy����������ϣ�OA=8��OC=4����P�ӵ�O��������x����ÿ��2����λ�����ٶ����A�����˶�������P�����Aʱֹͣ�˶������P�˶���ʱ����t�룮���߶�CP���е��Ƶ�P��˳ʱ�뷽����ת90��õ�D����D���P���˶����˶�������DP��DA������D��DQ��OA����OA�ڵ�Q���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
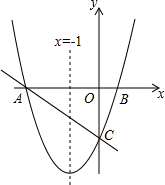 ��ͼ���Գ���Ϊֱ��x=-1��������y=ax2+bx+c��a��0����x���ཻ��A��B���㣬����A�������Ϊ��-3��0����CΪ��������y��Ľ�����S��ABC=6
��ͼ���Գ���Ϊֱ��x=-1��������y=ax2+bx+c��a��0����x���ཻ��A��B���㣬����A�������Ϊ��-3��0����CΪ��������y��Ľ�����S��ABC=6�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
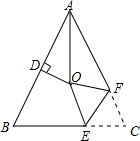 ��ͼ����ABC�У�AB=AC����BAC=54�㣬��BAC��ƽ������AB�Ĵ�ֱƽ���߽��ڵ�O������C��EF��E��BC�ϣ�F��AC�ϣ��۵�����C���Oǡ���غϣ����OECΪ108�ȣ�
��ͼ����ABC�У�AB=AC����BAC=54�㣬��BAC��ƽ������AB�Ĵ�ֱƽ���߽��ڵ�O������C��EF��E��BC�ϣ�F��AC�ϣ��۵�����C���Oǡ���غϣ����OECΪ108�ȣ��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com