
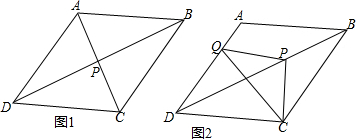
分析 (1)①首先根据菱形的特征,判断出∠CPD=90°,再根据∠CPQ=120°,判断出∠DPQ=30°;然后判断出∠ADP=30°,即可推得点Q是线段DP的垂直平分线与AD的交点;最后根据线段垂直平分线的作法作图即可.
②猜想PC与PQ的数量关系为:PC=PQ.首先根据∠DPQ=∠ADP=30°,求出∠AQP=60°,推得PA=PQ;然后判断出PC=PA,即可推得PC=PQ.
(2)首先根据∠CPQ=120°,∠CPD=80°,求出∠DPQ的度数是多少;然后在△DPQ中,根据三角形的内角和定理,求出∠PQD的度数是多少即可.
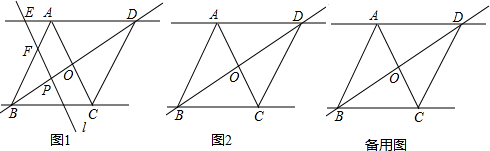
解答 解:(1)①如图1,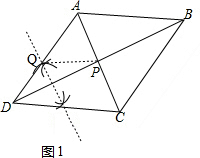 ,
,
∵点P为菱形ABCD的对角线的交点,
∴∠CPD=90°,
∵点Q在直线AD上,且∠CPQ=120°,
∴∠DPQ=120°-90°=30°,
又∵∠ABC=60°,
∴∠ADC=60°,
∴∠ADP=60°÷2=30°,
∴∠DPQ=∠ADP,
∴点Q是线段DP的垂直平分线与AD的交点.
②猜想PC与PQ的数量关系为:PC=PQ.
证明:如图2,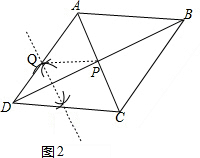 ,
,
∵∠DPQ=∠ADP=30°,
∴∠AQP=30°+30°=60°,
又∵∠QAP=∠APD-∠ADP=90°-30°=60°,
∴∠AQP=∠QAP,
∴PA=PQ,
又∵PC=PA,
∴PC=PQ.
(2)如图3,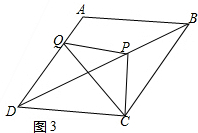 ,
,
∵∠CPQ=120°,∠CPD=80°,
∴∠DPQ=120°-80°=40°,
又∵∠ADP=30°,
∴∠PQD=180°-30°-40°=110°.
点评 (1)此题主要考查了四边形综合题,考查了分析推理能力,考查了数形结合思想的应用,要熟练掌握.
(2)此题还考查了菱形的性质和应用,要熟练掌握,解答此题的关键是要明确:①菱形具有平行四边形的一切性质;②菱形的四条边都相等; ③菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;④菱形是轴对称图形,它有2条对称轴,分别是两条对角线所在直线.
(3)此题还考查了三角形的内角和定理,要熟练掌握,解答此题的关键是要明确:三角形的内角和是180°.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
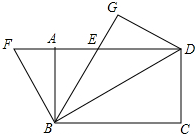 如图,矩形ABCD中,AB=2$\sqrt{3}$,BC=6,将该矩形沿对角线BD翻折,使△DBG与△DBC在同一平面内,C的对应点为G,BG交AD于点E,以BE为边作等边三角形PEF(P与B重合),点E、F位于AB两侧,将△PAF沿射线BD方向平移,当P到达点D时停止平移.当平移结束后,(即点P到达点D时),将△PAF绕点P顺时针旋转一个角度α(0<α<180°),A的对应点A′,F的对应点F′,直线PF′与直线BG的交点为M,直线F′A′与直线BG的交点为N,在旋转过程中,当△F′MN是直角三角形,且∠MNF′=90°时,则F′N的长度为2$\sqrt{3}$-2.
如图,矩形ABCD中,AB=2$\sqrt{3}$,BC=6,将该矩形沿对角线BD翻折,使△DBG与△DBC在同一平面内,C的对应点为G,BG交AD于点E,以BE为边作等边三角形PEF(P与B重合),点E、F位于AB两侧,将△PAF沿射线BD方向平移,当P到达点D时停止平移.当平移结束后,(即点P到达点D时),将△PAF绕点P顺时针旋转一个角度α(0<α<180°),A的对应点A′,F的对应点F′,直线PF′与直线BG的交点为M,直线F′A′与直线BG的交点为N,在旋转过程中,当△F′MN是直角三角形,且∠MNF′=90°时,则F′N的长度为2$\sqrt{3}$-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
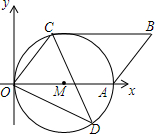 如图,在平面直角坐标系xOy中,点A在x轴正半轴上,OA=8,以OA为直径作⊙M,点C在⊙M上,∠AOC=45°,四边形ABCO为平行四边形.
如图,在平面直角坐标系xOy中,点A在x轴正半轴上,OA=8,以OA为直径作⊙M,点C在⊙M上,∠AOC=45°,四边形ABCO为平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com