
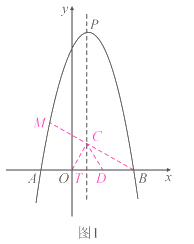
【题目】如图1,已知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,
,![]() .
.

(1)求抛物线的解析式;
(2)M为![]() 轴上方抛物线上的一点,
轴上方抛物线上的一点,![]() 与抛物线的对称轴交于点
与抛物线的对称轴交于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
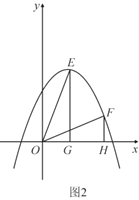
(3)如图2,将原抛物线沿对称轴平移后得到新抛物线为![]() ,
,![]() ,
,![]() 是新抛物线在第一象限内互不重合的两点,
是新抛物线在第一象限内互不重合的两点,![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() ,
,![]() ,若始终存在这样的点
,若始终存在这样的点![]() ,
,![]() ,满足
,满足![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)点
;(2)点![]() 坐标为
坐标为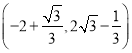 ;(3)
;(3)![]()
【解析】
(1)设![]() ,将点A的坐标代入求解即可;
,将点A的坐标代入求解即可;
(2)令![]() 求出点B的坐标,设抛物线对称轴直线
求出点B的坐标,设抛物线对称轴直线![]() 与
与![]() 轴交点为
轴交点为![]() ,作原点
,作原点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,根据已知条件可求出点C的坐标,根据待定系数法求出直线
,根据已知条件可求出点C的坐标,根据待定系数法求出直线![]() 的解析式,与抛物线解析式联立可求出点M的坐标;
的解析式,与抛物线解析式联立可求出点M的坐标;
(3)设![]() ,根据全等三角形的性质得出
,根据全等三角形的性质得出![]() ,设新抛物线解析式为
,设新抛物线解析式为![]() ,将点
,将点![]() 、
、![]() 的坐标代入抛物线的解析式得到两个等式,进而可得出m与n的关系,可先求出n的取值范围,最后根据h与n的函数关系式进行求解.
的坐标代入抛物线的解析式得到两个等式,进而可得出m与n的关系,可先求出n的取值范围,最后根据h与n的函数关系式进行求解.
解:(1)![]() 抛物线
抛物线![]() 的顶点为
的顶点为![]() ,
,
![]() ,
,
把![]() 代入抛物线解析式得,
代入抛物线解析式得,![]() ,
,
解得,![]() ,
,
![]() ;
;
(2)令![]() 得,
得,![]() ,
,
![]() 或
或![]() ,
,
![]() ,
,
![]() ,
,
设抛物线对称轴直线![]() 与
与![]() 轴交点为
轴交点为![]() ,作原点
,作原点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,则
,则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 设直线
设直线![]() 的解析式为
的解析式为![]() ,
,
则![]() ,
,![]() ,
,
解得![]() ,
,![]() ,
,
![]() 直线
直线![]() 解析式为
解析式为![]() ,
,
与抛物线![]() 联立得
联立得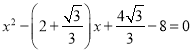 ,
,
![]() ,即
,即![]() ,
,
∴![]() ,
,
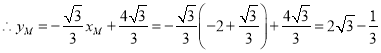 ,
,
故点![]() 坐标为
坐标为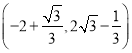 ;
;
(3)设![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
设新抛物线解析式为![]() ,
,
把点![]() 、
、![]() 的坐标代入抛物线的解析式得:
的坐标代入抛物线的解析式得:![]() ,
,![]() ,
,
即![]() ,
,![]() ,
,
建立![]() 与
与![]() 或
或![]() 与
与![]() 的函数关系式,从而求
的函数关系式,从而求![]() 的取值范围,
的取值范围,
先找到![]() 与
与![]() 的关系式,
的关系式,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() 且
且![]() ,
,
把![]() 代入
代入![]() 得
得![]() ,
,
![]() 且
且![]() ,
,
![]() ,
,
故![]() 的取值范围
的取值范围![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系xOy中,抛物线![]() 经过点A(5,0)、B(-3,4),抛物线的对称轴与x轴相交于点D.
经过点A(5,0)、B(-3,4),抛物线的对称轴与x轴相交于点D.
(1)求抛物线的表达式;
(2)联结OB、BD.求∠BDO的余切值;
(3)如果点P在线段BO的延长线上,且∠PAO =∠BAO,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】杨华与季红用5张同样规格的硬纸片做拼图游戏,正面如图1所示,背面完全一样,将它们背面朝上搅匀后,同时抽出两张.规则如下:当两张硬纸片上的图形可拼成电灯或小人时,杨华得1分;当两张硬纸片上的图形可拼成房子或小山时,季红得1分(如图2).问题:游戏规则对双方公平吗?请说明理由;若你认为不公平,如何修改游戏规则才能使游戏对双方公平?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形 ABCD 中,E 为 BC 边中点.
(Ⅰ)已知:如图,若 AE 平分∠BAD,∠AED=90°,点 F 为 AD 上一点,AF=AB.求证:(1)△ABE≌AFE;(2)AD=AB+CD

(Ⅱ)已知:如图,若 AE 平分∠BAD,DE 平分∠ADC,∠AED=120°,点 F,G 均为 AD上的点,AF=AB,GD=CD.求证:(1)△GEF 为等边三角形;(2)AD=AB+ ![]() BC+CD.
BC+CD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业销售某商品,以“线上”与“线下”相结合的方式一共销售了100件.设该商品线下的销售量为![]() 件,线下销售的每件利润为
件,线下销售的每件利润为![]() 元,线上销售的每件利润为
元,线上销售的每件利润为![]() 元.下图中折线
元.下图中折线![]() 、线段
、线段![]() 分别表示
分别表示![]() 与
与![]() 之间的函数关系.
之间的函数关系.
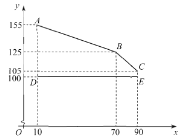
(1)当![]() 时,线上的销售量为_______件;
时,线上的销售量为_______件;
(2)求线段![]() 所表示的
所表示的![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(3)当线下的销售量为多少时,售完这100件商品所获得的总利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F,设PA=x。

(1)求证:△PFA∽△ABE;
(2)若以P,F,E为顶点的三角形也与△ABE相似,试求x的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
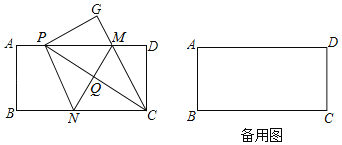
【题目】如图,现有一张矩形纸片ABCD,AB=4,BC=8,点M,N分别在矩形的边AD,BC上,将矩形纸片沿直线MN折叠,使点C落在矩形的边AD上,记为点P,点D落在G处,连接PC,交MN丁点Q,连接CM.
(1)求证:PM=PN;
(2)当P,A重合时,求MN的值;
(3)若△PQM的面积为S,求S的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式更多样、便捷某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息解答下列问题:
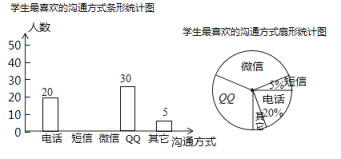
(1)这次统计共抽查了多少名学生?在扇形统计图中,表示" ![]() "的扇形圆心角的度数是多少;
"的扇形圆心角的度数是多少;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用 “微信”进行沟通的学生大约有多少名?
(4)某天甲、乙两名同学都想从“微信"、"![]() "、“电话"三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
"、“电话"三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com