
【题目】已知:在平面直角坐标系xOy中,抛物线![]() 经过点A(5,0)、B(-3,4),抛物线的对称轴与x轴相交于点D.
经过点A(5,0)、B(-3,4),抛物线的对称轴与x轴相交于点D.
(1)求抛物线的表达式;
(2)联结OB、BD.求∠BDO的余切值;
(3)如果点P在线段BO的延长线上,且∠PAO =∠BAO,求点P的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点P的坐标为(
;(3)点P的坐标为(![]() ,
,![]() ).
).
【解析】
(1)根据点A,B的坐标,利用待定系数法可求出抛物线的表达式;
(2)利用二次函数的性质可得出抛物线的对称轴,进而可得出点D的坐标,过点B作BC⊥x轴,垂足为点C,由点B,D的坐标可得出CD,BC的长度,结合余切的定义可求出∠BDO的余切值;
(3)设点P的坐标为(m,n),过点P作PQ⊥x轴,垂足为点Q,则PQ=﹣n,OQ=m,AQ=5﹣m,在Rt△ABC中,可求出cot∠∠BAC=2,结合∠PAO=∠BAO可得出m﹣2n=5①,由BC⊥x轴,PQ⊥x轴可得出BC∥PQ,进而可得出4m=﹣3n②,联立①②可得出点P的坐标.
解:(1)∵ 抛物线![]() 经过点A(5,0)、B(-3,4),
经过点A(5,0)、B(-3,4),
∴ ![]()
解得 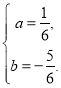
∴ 所求抛物线的表达式为![]() .
.
(2)由![]() ,得抛物线的对称轴为直线
,得抛物线的对称轴为直线![]() .
.
∴ 点D(![]() ,0).
,0).
过点B作BC⊥x轴,垂足为点C.
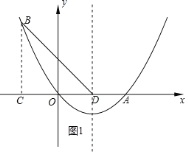
由A(5,0)、B(-3,4),得 BC = 4,OC = 3,![]() .
.
∴ ![]() .
.
(3)设点P(m,n).
过点P作PQ⊥x轴,垂足为点Q.则 PQ = -n,OQ = m,AQ = 5 – m.

在Rt△ABC中,∠ACB = 90°,∴ ![]() .
.
∵ ∠PAO =∠BAO,∴ ![]() .
.
即得 ![]() . ①
. ①
由 BC⊥x轴,PQ⊥x轴,得 ∠BCO =∠PQA = 90°.
∴ BC // PQ.
∴ ![]() ,即得
,即得 ![]() .∴ 4 m = - 3 n. ②
.∴ 4 m = - 3 n. ②
由 ①、②解得 ![]() ,
,![]() .
.
∴ 点P的坐标为(![]() ,
,![]() ).
).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】四边形![]() 为矩形,连接
为矩形,连接![]() ,
,![]() ,点
,点![]() 在
在![]() 边上.
边上.
(1)如图①,若![]() ,
,![]() ,求
,求![]() 的面积;
的面积;
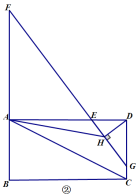
(2)如图②,延长![]() 至点
至点![]() ,使得
,使得![]() ,连接
,连接![]() 并延长交
并延长交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证:![]() ;
;
(3)如图③,将线段![]() 绕点
绕点![]() 旋转一定的角度
旋转一定的角度![]() (
(![]() )得到线段
)得到线段![]() ,连接
,连接![]() ,点
,点![]() 始终为
始终为![]() 的中点,连接
的中点,连接![]() .已知
.已知![]() ,直接写出
,直接写出![]() 的取值范围.
的取值范围.


查看答案和解析>>
科目:初中数学 来源: 题型:
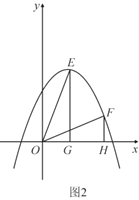
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣![]() x+4与x轴交于A、B两点(A点在B点左侧),与y轴交于点C,且点B的坐标为(4,0),点E(m,0)为x轴上的一个动点,过点E作直线l⊥x轴,与抛物线y=ax2﹣
x+4与x轴交于A、B两点(A点在B点左侧),与y轴交于点C,且点B的坐标为(4,0),点E(m,0)为x轴上的一个动点,过点E作直线l⊥x轴,与抛物线y=ax2﹣![]() x+4交于点F,与直线AC交于点G.
x+4交于点F,与直线AC交于点G.
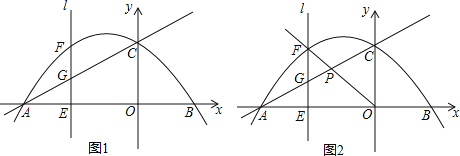
(1)分别求抛物线y=ax2﹣![]() x+4和直线AC的函数表达式;
x+4和直线AC的函数表达式;
(2)当﹣8<m<0时,求出使线段FG的长度为最大值时m的值;
(3)如图2,作射线OF与直线AC交于点P,请求出使FP:PO=1:2时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
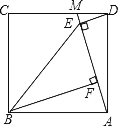
【题目】如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点E,BF⊥AM于点F,连接BE,若AF=1,四边形ABED的面积为6,则∠EBF的余弦值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB = 90°,BC = 3,AC = 4,点D为边AB上一点.将△BCD沿直线CD翻折,点B落在点E处,联结AE.如果AE // CD,那么BE =________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
|
|
|
|
|
| |
七年级 | 0 | 1 | 0 | a | 7 | 1 |
八年级 | 1 | 0 | 0 | 7 | b | 2 |
分析数据:
平均数 | 众数 | 中位数 | |
七年级 | 78 | 75 |
|
八年级 | 78 |
| 80.5 |
应用数据:
(1)由上表填空:a= ,b= ,c= ,d= .
(2)估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?
(3)你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
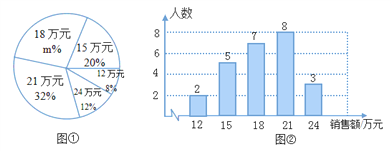
【题目】某商场服装部分为了解服装的销售情况,统计了每位营业员在某月的销售额(单位:万元),并根据统计的这组销售额的数据,绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
该商场服装营业员的人数为 ,图①中m的值为 ;
求统计的这组销售额数据的平均数、众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
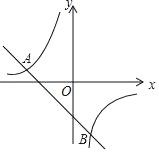
【题目】如图,一次函数y1=kx+b(k≠0)和反比例函数![]() 的图象相交于点A(﹣4,2),B(n,﹣4)
的图象相交于点A(﹣4,2),B(n,﹣4)
(1)求一次函数和反比例函数的表达式;
(2)观察图象,直接写出不等式y1<y2的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴的交点为
轴的交点为![]() ,
,![]() .
.

(1)求抛物线的解析式;
(2)M为![]() 轴上方抛物线上的一点,
轴上方抛物线上的一点,![]() 与抛物线的对称轴交于点
与抛物线的对称轴交于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图2,将原抛物线沿对称轴平移后得到新抛物线为![]() ,
,![]() ,
,![]() 是新抛物线在第一象限内互不重合的两点,
是新抛物线在第一象限内互不重合的两点,![]() 轴,
轴,![]() 轴,垂足分别为
轴,垂足分别为![]() ,
,![]() ,若始终存在这样的点
,若始终存在这样的点![]() ,
,![]() ,满足
,满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com