
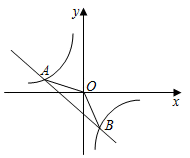
【题目】如图,一次函数y=﹣x+b的图象与反比例函数y=![]() 的图象交于A、B两点,且A点坐标为(﹣2,1),一次函数交x轴于点C.
的图象交于A、B两点,且A点坐标为(﹣2,1),一次函数交x轴于点C.
(1)试确定上述反比例函数和一次函数的表达式;
(2)求△AOB的面积;
(3)直接写出使反比例函数大于一次函数的x的取值范围.
【答案】(1)反比例函数解析式为y=﹣![]() ,一次函数解析式为y=﹣x﹣1;(2)
,一次函数解析式为y=﹣x﹣1;(2)![]() ;(3)﹣2<x<0或x>1
;(3)﹣2<x<0或x>1
【解析】
(1)把A(﹣2,1)代入y=﹣x+b中,求出b,得到一次函数解析式;然后把A(﹣2,1)代入y=![]() 中,求出m,得到反比例函数解析式;
中,求出m,得到反比例函数解析式;
(2)先求出直线y=﹣x﹣1与y轴的交点坐标,再联立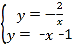 ,求出点B的坐标,然后利用三角形面积公式计算△AOB的面积,即可;
,求出点B的坐标,然后利用三角形面积公式计算△AOB的面积,即可;
(3)结合图象写出反比例函数图象在一次函数图象上方对应的自变量的范围即可.
(1)把A(﹣2,1)代入y=﹣x+b,得2+b=1,解得:b=﹣1,
∴一次函数解析式为:y=﹣x﹣1;
把A(﹣2,1)代入y=![]() ,得:m=﹣2×1=﹣2,
,得:m=﹣2×1=﹣2,
∴反比例函数解析式为:y=﹣![]() ;
;
(2)当x=0时,y=﹣x﹣1=﹣1,则直线y=﹣x﹣1与y轴的交点坐标为(0,﹣1),
联立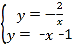 ,得:﹣
,得:﹣![]() =﹣x﹣1,
=﹣x﹣1,
解得:![]() ,
,
∴B(1,-2),
∴△AOB的面积=![]() ×1×(2+1)=
×1×(2+1)=![]() ;
;
(3)根据函数图象,反比例函数图象在一次函数图象上方所对应的自变量的范围是:﹣2<x<0或x>1.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.

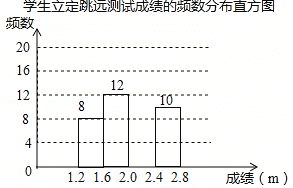
请根据图表中所提供的信息,完成下列问题:
(1)表中![]() ________,
________,![]() ________,样本成绩的中位数落在证明见解析________范围内;
________,样本成绩的中位数落在证明见解析________范围内;
(2)请把频数分布直方图补充完整;
(3)该校九年级共有1000名学生,估计该年级学生立定跳远成绩在![]() 范围内的学生有多少人?
范围内的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=kx+b与反比例函数y2=![]() 的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
的图象交于A(2,3),B(6,n)两点,与x轴、y轴分别交于C,D两点.
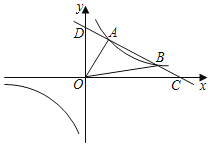
(1)求一次函数与反比例函数的解析式.
(2)求当x为何值时,y1>0.
查看答案和解析>>
科目:初中数学 来源: 题型:
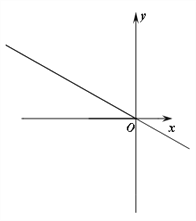
【题目】已知二次函数![]() >0)的对称轴与x轴交于点B,与直线l:
>0)的对称轴与x轴交于点B,与直线l:![]() 交于点C,点A是该二次函数图像与直线l在第二象限的交点,点D是抛物线的顶点,已知AC∶CO=1∶2,∠DOB=45°,△ACD的面积为2.
交于点C,点A是该二次函数图像与直线l在第二象限的交点,点D是抛物线的顶点,已知AC∶CO=1∶2,∠DOB=45°,△ACD的面积为2.
(1) 求抛物线的函数关系式;
(2) 若点P为抛物线对称轴上的一个点,且∠POC=45°,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系,点 O 是原点,直线 y x 6分别交 x 轴,y 轴于点 B,A,经过点 A 的直线 y x b 交 x 轴于点 C.
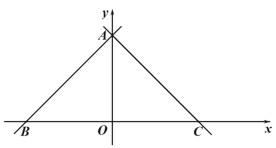
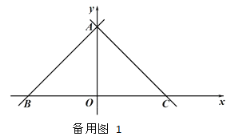
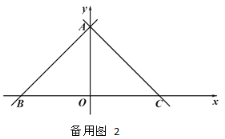
(1)求 b 的值 ;
(2)点 D 是线段 AB 上的一个动点,连接 OD,过点 O 作 OE⊥OD 交 AC 于点 E,连接DE,将△ODE 沿 DE 折叠得到△FDE,连接 AF.设点 D 的横坐标为 t,AF 的长为 d,当t> 3 时,求 d 与 t 之间的函数关系式(不要求写出自变量 t 的取值范围);
(3)在(2)的条件下,DE 交 OA 于点 G,且 tan∠AGD=3.点 H 在 x 轴上(点 H 在点O 的右侧),连接 DH,EH,FH,当∠DHF=∠EHF 时,请直接写出点 H 的坐标,不需要写出解题过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了更好的治理西流湖水质,保护环境,市治污公司决定购买 10 台污水处理设备.现有 A、B 两种型号的设备,其中每台的价格,月处理污水量如下表:
A 型 | B 型 | |
价格(万元/台) | a | b |
处理污水量(吨/月) | 240 | 200 |
经调查:购买一台 A 型设备比购买一台 B 型设备多 2 万元,购买 2 台 A 型设备比购买 3 台 B 型设备少 6 万元.
(1)求 a,b 的值;
(2)经预算:市治污公司购买污水处理设备的资金不超过 105 万元,你认为该公司 有哪几种购买方案;
(3)在(2)问的条件下,若每月要求处理西流湖的污水量不低于 2040 吨,为了节 约资金,请你为治污公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请仅用无刻度的直尺完成下列画图,不写画法,保留画图痕迹.(用虚线表示画图过程,实线表示画图结果)
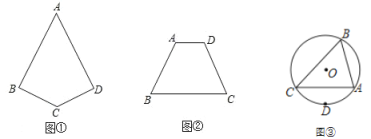
(1)如图①,四边形 ABCD 中,AB=AD,∠B=∠D,画出四边形 ABCD 的对称轴 m;
(2)如图②,四边形 ABCD 中,AD∥BC,∠A=∠D,画出 BC 边的垂直平分线 n.
(3)如图③,△ABC 的外接圆的圆心是点 O,D 是![]() 的中点,画一条直线把△ABC 分成面积相等的两部分.
的中点,画一条直线把△ABC 分成面积相等的两部分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】参照学习函数的过程方法,探究函数![]() 的图像与性质,因为
的图像与性质,因为![]() ,即
,即![]() ,所以我们对比函数
,所以我们对比函数![]() 来探究列表:
来探究列表:
| … | -4 | -3 | -2 | -1 |
|
| 1 | 2 | 3 | 4 | … | |
| … |
|
| 1 | 2 | 4 | -4 | -2 | -1 |
|
| … | |
| … |
|
| 2 | 3 | 5 | -3 | -2 | 0 |
|
| … |
描点:在平面直角坐标系中以自变量![]() 的取值为横坐标,以
的取值为横坐标,以![]() 相应的函数值为纵坐标,描出相应的点如图所示:
相应的函数值为纵坐标,描出相应的点如图所示:
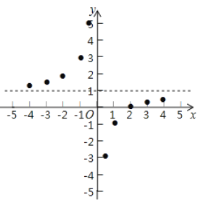
(1)请把![]() 轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;
轴左边各点和右边各点分别用一条光滑曲线,顺次连接起来;
(2)观察图象并分析表格,回答下列问题:
①当![]() 时,
时,![]() 随
随![]() 的增大而______;(“增大”或“减小”)
的增大而______;(“增大”或“减小”)
②![]() 的图象是由
的图象是由![]() 的图象向______平移______个单位而得到的;
的图象向______平移______个单位而得到的;
③图象关于点______中心对称.(填点的坐标)
(3)函数![]() 与直线
与直线![]() 交于点
交于点![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐场新推出了一个“极速飞车”的项目.项目有两条斜坡轨道以满足不同的难度需求,游客可以乘坐垂直升降电梯AB自由上下选择项目难度.其中斜坡轨道BC的坡度(或坡比)为i=1:2,BC=12![]() 米,CD=8米,∠D=36°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为( )米.(精确到0.1米,参考数据:tan36°≈0.73,cos36°≈0.81,sin36°≈0.59)
米,CD=8米,∠D=36°,(其中点A、B、C、D均在同一平面内)则垂直升降电梯AB的高度约为( )米.(精确到0.1米,参考数据:tan36°≈0.73,cos36°≈0.81,sin36°≈0.59)
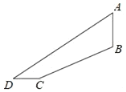
A.5.6B.6.9C.11.4D.13.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com