
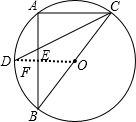
 如图.Rt△ABC内接于⊙O,BC为直径,AB=4,AC=3,D是
如图.Rt△ABC内接于⊙O,BC为直径,AB=4,AC=3,D是 |
| AB |
| CE |
| DE |
 |
| AB |
| CE |
| DE |
| AC |
| DF |
| CE |
| DE |
| 3 |
| 1 |


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:初中数学 来源: 题型:
| 30 |
| 3 |
| 2 |
2
|
2
|
| 2 |
| b |
| ab5 |
| 6a |
| b2 |
|
| 3 |
| 2 |
| a3b |
| 7 |
|
| 3 |
| 2 |
2
|
| ab3 |
|
| 2a |
| 3 |
| 3 |
| 27 |
| 54 |
| 6 |
| 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:
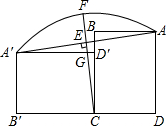 如图,将矩形ABCD向左绕点C推倒,恰好D落在BC上D′处,得到矩形A′B′C′D′,作CE⊥AA′交
如图,将矩形ABCD向左绕点C推倒,恰好D落在BC上D′处,得到矩形A′B′C′D′,作CE⊥AA′交 |
| AA′ |
查看答案和解析>>
科目:初中数学 来源: 题型:
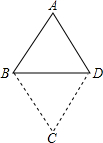 如图,将等边△ABD沿BD中点旋转180°得到△BDC.现给出下列命题:
如图,将等边△ABD沿BD中点旋转180°得到△BDC.现给出下列命题:查看答案和解析>>
科目:初中数学 来源: 题型:
| A、225 | B、240 |
| C、30 | D、255 |
查看答案和解析>>
科目:初中数学 来源: 题型:
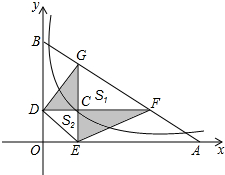 如图,已知动点C在函数y=
如图,已知动点C在函数y=| 6 |
| x |
| 4 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com